Question

点P是以F₁、F₂为焦点的双曲线E:(a＞0，b＞0)上的一点，已知PF₁⊥PF₂，,O为坐标原点．

(Ⅰ)求双曲线的离心率e；

(Ⅱ)过点P作直线分别与双曲线两渐近线相交于P₁、P₂两点，且，=0,求双曲线E的方程；

(Ⅲ)若过点Q(m，0)(m为非零常数)的直线l与(Ⅱ)中的双曲线E相交于不同于双曲线顶点的两点M、N，且(λ为非零实数)，问在x轴上是否存在定点G，使?若存在，求出所有这种定点G的坐标；若不存在，请说明理由．

Answer 1

解：(Ⅰ)∵|PF₁|=2|PF₂|,|PF₁|-|PF₂|=2a,

∴|PF₁|=4a,|PF₂|=2a

∵PF₁⊥PF₂,∴(4a)²+(2a)²=(2c)²,  ∴e= 

(Ⅱ)由(Ⅰ)知双曲线的方程可设为,渐近线方程为y=±2x

设P₁(x₁,2x₁),P₂(x₂,-2x₂),P(x,y)  ∵=-3x₁x₂=-

∵2 

∵点P在双曲线上，∴

化简得x₁x₂=,∴=a²=2

∴双曲线方程为 

(Ⅲ)设在x轴上存在定点G（t,0）,使

i)若直线l⊥x轴时，|m|＞（确保直线l与双曲线E有两个不同交点）

λ=1时，则有且对x轴上任一点G,

 

ii)若直线l不垂直x轴时，设直线l:y=k(x-m),M(x₃,y₃),M(x₄,y₄)

联立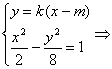(4-k²)x²+2k²mx-k²m²-8=0 

x₃x₄=  ∵

⊥()的充要条件为x₃-t-λx₄+λt=0

由=λy₃+λy₄=0λ=-

又∵y₃=k(x₃-m),y₄=k(x₄-m)  ∴x₃-t-λx₄+λt=x₃-t+

x₃-t+

2x₃x₄-(x₃+x₄)(m+t)+2mt=0

mt=2t=

综上:在x轴上存在一点G(,0),使.