
如图,在几何体 中,点
中,点 在平面ABC内的正投影分别为A,B,C,且
在平面ABC内的正投影分别为A,B,C,且 ,
, ,E为
,E为 中点,
中点,

(1)求证;CE∥平面 ,
,
(2)求证:求二面角 的大小.
的大小.
(1)详见解析;(2)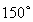 .
.
【解析】
试题分析:(1)通过证明线线平行,证明线面平行,所以取 的中点
的中点 ,连接
,连接 ,通过证明
,通过证明 ,从而证明
,从而证明 ;(2)首先建立空间直角坐标系,分别求出平面
;(2)首先建立空间直角坐标系,分别求出平面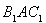 与平面
与平面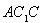 的法相量
的法相量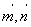 ,即利用
,即利用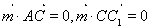 ,求出
,求出 ,利用
,利用 ,求出
,求出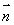 ,然后利用公式
,然后利用公式 注意由实际图像看为钝二面角,从而求出二面角
注意由实际图像看为钝二面角,从而求出二面角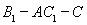 的大小.考察内容比较基础,证明时严格按照判定定理,逻辑性严谨.
的大小.考察内容比较基础,证明时严格按照判定定理,逻辑性严谨.
试题解析:(1)由题意知:

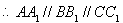 1分
1分
取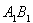 中点
中点 ,连
,连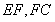 ,
,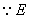 为
为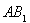 中点,
中点,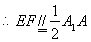
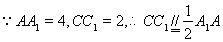
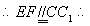 四边形
四边形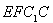 为平行四边形
为平行四边形
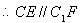 4分
4分
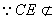 面
面 ,
,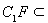 面
面
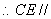 面
面 5分
5分
(2)由题知 又
又 分别以
分别以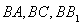 所在直线为
所在直线为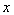 轴,
轴,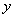 轴,
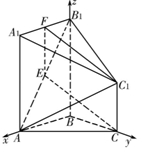
轴, 轴建立如图所示空间直角坐标系.
轴建立如图所示空间直角坐标系.
则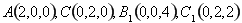 ,
,
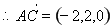


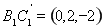
设平面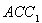 法相量
法相量 ;则
;则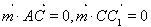
 ,令
,令 ,得
,得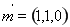
设平面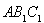 法相量
法相量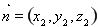 ;则
;则
 ,令
,令 ,则
,则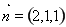 10分
10分

由图知二面角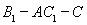 为钝角
为钝角
所以二面角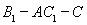 的大小为
的大小为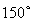
考点:1.线面平行的判定定理;2.向量法求二面角的大小.


科目:高中数学 来源: 题型:
 如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点.
如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
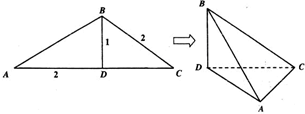 如图,在△ABC中,BD为AC边上的高,BD=1,BC=AD=2,沿BD将△ABD翻折,使得∠ADC=30°,得几何体B-ACD
如图,在△ABC中,BD为AC边上的高,BD=1,BC=AD=2,沿BD将△ABD翻折,使得∠ADC=30°,得几何体B-ACD查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省潍坊市高三上学期期末考试文科数学试卷(解析版) 题型:解答题
如图,在几何体 中,点
中,点 在平面ABC内的正投影分别为A,B,C,且
在平面ABC内的正投影分别为A,B,C,且 ,E为
,E为 中点,
中点, .
.

(1)求证;CE∥平面 ,
,
(2)求证:平面 平面
平面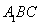
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省三明市毕业班5月质量检查理科数学试卷(解析版) 题型:解答题
如图,在几何体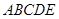 中,
中,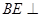 平面
平面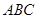 ,
,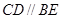 ,
,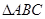 是等腰直角三角形,
是等腰直角三角形,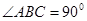 ,且
,且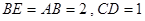 ,点
,点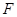 是
是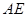 的中点.
的中点.

(Ⅰ)求证: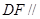 平面
平面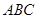 ;
;
(Ⅱ)求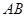 与平面
与平面 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com