
 .如图所示给出一个“三角形数阵”,已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为aij(i≥j,j∈N+),则a83=( )
.如图所示给出一个“三角形数阵”,已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为aij(i≥j,j∈N+),则a83=( ) 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源:2012-2013学年浙江省高三下学期回头考文科数学试卷(解析版) 题型:选择题
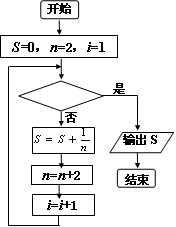
如图所示给出的是计算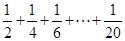 的值的一个程序框图,其中判断框内可以填的条件是( )
的值的一个程序框图,其中判断框内可以填的条件是( )
A.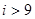 B.
B.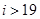 C.
C.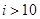 D.
D.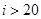
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
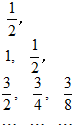 .如图所示给出一个“三角形数阵”,已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为aij(i≥j,j∈N+),则a83=
.如图所示给出一个“三角形数阵”,已知每一列的数成等差数列,从第三行起,每一行的数成等比数列,每一行的公比都相等,记第i行第j列的数为aij(i≥j,j∈N+),则a83=


查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省安庆市望江四中高三(上)第四次月考数学试卷(文科)(解析版) 题型:选择题
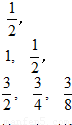



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com