
已知A,B两点在抛物线C:x2=4y上,点M(0,4)满足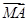 =λ
=λ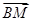 .
.
(1)求证: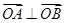 ;
;
(2)设抛物线C过A、B两点的切线交于点N.
(ⅰ)求证:点N在一条定直线上;
(ⅱ)设4≤λ≤9,求直线MN在x轴上截距的取值范围.
(1)证明:∵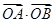 =0,∴
=0,∴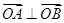 .
.
(2)(ⅰ)点N(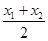 ,-4),所以点N在定直线y=-4上. (ⅱ) [-
,-4),所以点N在定直线y=-4上. (ⅱ) [- ,-
,-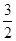 ]∪[
]∪[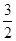 ,
, ].
].
【解析】
试题分析:设A(x1,y1),B(x2,y2),
lAB:y=kx+4与x2=4y联立得x2-4kx-16=0,
Δ=(-4k)2-4(-16)=16k2+64>0,
x1+x2=4k,x1x2=-16, 2分
(1)证明:∵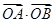 =x1x2+y1y2=x1x2+(kx1+4)(kx2+4)
=x1x2+y1y2=x1x2+(kx1+4)(kx2+4)
=(1+k2)x1x2+4k(x1+x2)+16
=(1+k2)(-16)+4k(4k)+16=0
∴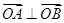 .
4分
.
4分
(2)(ⅰ)证明:过点A的切线:
y=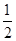 x1(x-x1)+y1=
x1(x-x1)+y1=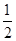 x1x-
x1x-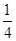 x12, ①
x12, ①
过点B的切线:y=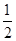 x2x-
x2x-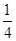 x22, ②
6分
x22, ②
6分
联立①②得点N(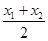 ,-4),所以点N在定直线y=-4上.
8分
,-4),所以点N在定直线y=-4上.
8分
(ⅱ)∵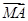 =λ
=λ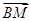 ,
,
∴(x1,y1-4)=λ(-x2,4-y2),
联立x1=-λx2,x1+x2=4k,x1x2=-16,
可得k2=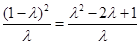 =λ+
=λ+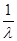 -2,4≤λ≤9,
11分
-2,4≤λ≤9,
11分
∴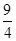 ≤k2≤
≤k2≤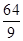 .
.
直线MN:y=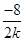 x+4在x轴上的截距为k.
x+4在x轴上的截距为k.
∴直线MN在x轴上截距的取值范围是[- ,-
,-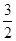 ]∪[
]∪[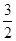 ,
, ]. 14分
]. 14分
考点:本题考查了向量的运用及直线与抛物线的位置关系
点评:熟练掌握向量的坐标运算,灵活运用直线的特征是解决此类问题的关键,属常考题型


科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,抛物E与直ly=k(x+1)(k∈R)相交于A、B两点.
,抛物E与直ly=k(x+1)(k∈R)相交于A、B两点. 时,求k的值.
时,求k的值.查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆![]() 是抛物
是抛物
线![]() 的一条切线.
的一条切线.
(I)求椭圆的方程;
(II)过点![]() 的动直线L交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,请说明理由.
的动直线L交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省台州市天台县平桥中学高二(上)12月诊断数学试卷(理科)(解析版) 题型:解答题
 ,抛物E与直ly=k(x+1)(k∈R)相交于A、B两点.
,抛物E与直ly=k(x+1)(k∈R)相交于A、B两点.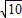 时,求k的值.
时,求k的值.查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省台州市天台县平桥中学高二(上)12月诊断数学试卷(文科)(解析版) 题型:解答题
 ,抛物E与直ly=k(x+1)(k∈R)相交于A、B两点.
,抛物E与直ly=k(x+1)(k∈R)相交于A、B两点. 时,求k的值.
时,求k的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com