
| |||||||||||||||
(1) |
解析:已知A1E⊥B1B于E,A1F⊥C1C于F,∵B1B∥C1C,∴B1B⊥A1F 又A1E∩A1F=A1,∴B1B⊥平面A1EF. ∴平面A1EF⊥平面B1BCC1. |
(2) |
∵∠A1B1B=∠A1AB=∠A1AC=∠A1C1C= 又∠A1EB1=∠A1FC1= ∴Rt△A1B1E≌Rt△A1C1F,∴A1E=A1F= ∴B1E∥C1F,∴EF=B1C1=2. ∴A1E2+A1F2=EF2, ∴△A1EF为等腰直角三角形. 取EF的中点N,连结A1N,则A1N⊥EF,∴A1N⊥平面B1BCC1. ∴A1N为点A1到平面B1BCC1的距离. 又A1N= 所以点A1到平面B1BCC1的距离为1. |
(3) |
如图所示,设BC、B1C1的中点分别为D、D1,连结AD、DD1和A1D1,则N∈DD1.
∵DD1∥BB1∥AA1,∴A、A1、D、D1四点共面,∴AD∥A1D1,∴四边形A1ADD1为平行四边形. ∵B1C1⊥A1D1,A1N⊥平面BCC1B1, ∴B1C1⊥D1D,又B1C1⊥A1N, ∴B1C1⊥平面ADD1A1. ∴BC⊥平面ADD1A. ∴平面A1ADD1⊥平面ABC. 作A1M⊥平面ABC于M,则点M在AD上. 若A1M=AN,又∠A1AD=∠A1D1D,∠A1MA=∠A1ND1= 则Rt△A1MA ≌ Rt△A1ND1. 于是A1A=A1D1= 即当A1A= 点评:本题中点到平面的距离用垂面法,理论依据是面面垂直的性质定理. |


科目:高中数学 来源: 题型:
 如图所示,已知三棱柱ABC-A1B1C1的各棱长均为2,侧棱B1B与底面ABC所成的角为,且侧面ABB1A1垂直于底面ABC.
如图所示,已知三棱柱ABC-A1B1C1的各棱长均为2,侧棱B1B与底面ABC所成的角为,且侧面ABB1A1垂直于底面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,已知三棱柱A′B′C′-ABC的侧棱垂直于底面,AC⊥CB,且AC=CB=CC′=2.若点E为A′B′中点,则CE与底面ABC所成角的余弦值为
如图所示,已知三棱柱A′B′C′-ABC的侧棱垂直于底面,AC⊥CB,且AC=CB=CC′=2.若点E为A′B′中点,则CE与底面ABC所成角的余弦值为
| ||
| 3 |
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省四校高三上学期期末联考文科数学 题型:选择题
如图所示,已知三棱柱 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 上的
上的
射影D为 的中点,则异面直线
的中点,则异面直线 与
与 所成的角的余弦值为( )
所成的角的余弦值为( )
A. B.
B.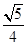 C.
C. D.
D.

查看答案和解析>>
科目:高中数学 来源:2010-2011年山东省高二下学期期中考试数学试卷(A) 题型:解答题
((本小题满分12分)
如图所示,已知三棱柱 ,在某个空间直角坐标系中,
,在某个空间直角坐标系中,
 ,
, ,其中
,其中 、
、

(1)证明:三棱柱 是正三棱柱;
是正三棱柱;
(2)若 ,求直线
,求直线 与平面
与平面 所成角的大小。
所成角的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com