
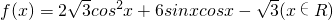 ,
,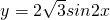 的图象经过怎样的变换得到的;
的图象经过怎样的变换得到的; 时,求函数f(x)的最值,并求出函数取最值时的x的值.
时,求函数f(x)的最值,并求出函数取最值时的x的值. (1+cos2x)+3sin2x-
(1+cos2x)+3sin2x-
 (cos2x+
(cos2x+ sin2x)
sin2x) sin(2x+
sin(2x+ )
) +2kπ≤2x+
+2kπ≤2x+ ≤
≤ +2kπ,k∈Z
+2kπ,k∈Z +kπ,
+kπ, +kπ],k∈Z
+kπ],k∈Z sin2x向左平移
sin2x向左平移 得到y=2
得到y=2 sin(2x+
sin(2x+ )
) ]
] ∈[
∈[ ,
, ]
] )∈[-
)∈[- ,1]
,1] =
= ,即x=
,即x= 时,f(x)min=-
时,f(x)min=- ,
, =
= ,即x=
,即x= 时,f(x)max=2
时,f(x)max=2 .
. sin(2x+
sin(2x+ ),进而得到单调递减区间;y=2
),进而得到单调递减区间;y=2 sin2x向左平移
sin2x向左平移 得到y=2
得到y=2 sin(2x+
sin(2x+ );
); 时,,求出2x+
时,,求出2x+ 的范围,进而得到sin(2x+
的范围,进而得到sin(2x+ )的范围,从而得到函数f(x)的 范围,从而求得函数f(x)的最大值.
)的范围,从而得到函数f(x)的 范围,从而求得函数f(x)的最大值.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源:2012-2013学年江西省吉安二中高三(上)第二轮周考数学试卷(理科)(解析版) 题型:解答题
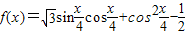 .
.查看答案和解析>>
科目:高中数学 来源:2010年湖北省襄阳市襄樊四中高考适应性考试数学试卷(文科)(解析版) 题型:解答题
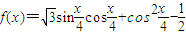 .
.查看答案和解析>>
科目:高中数学 来源:2007-2008学年湖北省部分重点中学高三第二次联考数学试卷(理科)(解析版) 题型:解答题
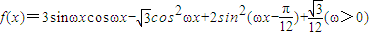 .
.查看答案和解析>>
科目:高中数学 来源:2012--2013学年河南省高一上学期第一次考试数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知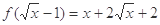 ,
,
(1)求函数f(x)的表达式?
(2)求函数f(x)的定义域?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com