
对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某市的教育研究机构对全市高三学生进行综合素质测试,随机抽取了部分学生的成绩,得到如图所示的成绩频率分布直方图.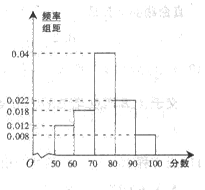
(I )估计全市学生综合素质成绩的平均值;
(II)若综合素质成绩排名前5名中,其中1人为某校的学生会主席,从这5人中推荐3人参加自主招生考试,试求这3人中含该学生会主席的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
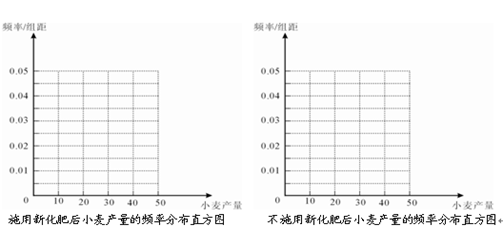
(本题12分)为了研究化肥对小麦产量的影响,某科学家将一片土地划分成200个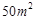 的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
表1:施用新化肥小麦产量频数分布表
| 小麦产量 | 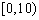 | 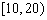 | 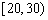 | 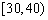 | 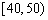 |
| 频数 | 10 | 35 | 40 | 10 | 5 |
| 小麦产量 | 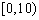 | 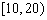 | 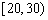 | 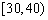 |
| 频数 | 15 | 50 | 30 | 5 |
| | 小麦产量小于20kg | 小麦产量不小于20kg | 合计 |
| 施用新化肥 | 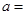 | 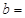 | |
| 不施用新化肥 | 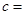 |  | |
| 合计 | | | 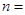 |
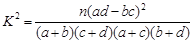
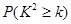 | 0.050 | 0.010 | 0.005 | 0.001 |
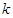 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1:
| 生产能力分组 | 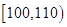 | 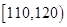 | 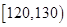 | 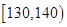 | 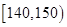 |
| 人数 | 4 | 8 |  | 5 | 3 |
| 生产能力分组 | 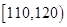 | 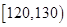 | 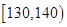 | 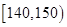 |
| 人数 | 6 | y | 36 | 18 |
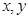 ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)(注意:本题请在答题卡上作图)
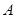 类工人和
类工人和 类工人生产能力的众数、中位数和平均数。(精确到0.1)
类工人生产能力的众数、中位数和平均数。(精确到0.1)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)为了调查甲、乙两个交通站的车流量,随机选取了14天,统计每天上午8∶00~12∶00间各自的车流量(单位:百辆),得如图所示的统计图,试求: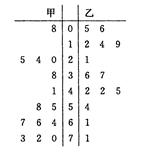
(1)甲、乙两个交通站的车流量的极差分别是多少?
(2)甲交通站的车流量在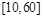 间的频率是多少?
间的频率是多少?
(3)根据该茎叶图结合所学统计知识分析甲、乙两个交通站哪个站更繁忙?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某班50位学生期中考试数学成绩的频率分布直方图如图所示,成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
(Ⅰ)求图中 x的值;
(Ⅱ)从成绩不低于80分的学生中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有一个容量为100的样本,数据的分组及各组的频数如下:
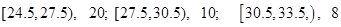
(1)列出样本的频率分布表;(2)画出频率分布直方图和频率折线图;(3)由直方图确定样本的中位数。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了调查胃病是否与生活规律有关,在某地对 名
名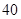 岁以上的人进行了调查,结果是:患胃病者生活不规律的共
岁以上的人进行了调查,结果是:患胃病者生活不规律的共 人,患胃病者生活规律的共
人,患胃病者生活规律的共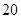 人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共
人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共 人.
人.
(1)根据以上数据列出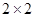 列联表.
列联表.
(2)并判断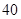 岁以上的人患胃病与否和生活规律是否有关。
岁以上的人患胃病与否和生活规律是否有关。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个总体中的1000个个体编号为0,1,2,…,999,并依次将其分为10个小组,组号为0,1,2,…,9,要用系统抽样方法抽取一个容量为10的样本,规定如果在第0组随机抽取的号码为x,那么依次错位地得到后面各组的号码,即第k组中抽取的号码的后两位数为x+33k的后两位数.
(1)当x=24时,写出所抽取样本的10个号码;
(2)若所抽取样本的10个号码中有一个的后两位数是87,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com