

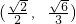


 ,直线AB方程为y=kx+b(k>0),两方程联解得到B的横坐标为-
,直线AB方程为y=kx+b(k>0),两方程联解得到B的横坐标为-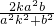 ,从而得|AB|=
,从而得|AB|= •
•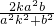 ,同理得到|AC|=
,同理得到|AC|=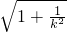 •
•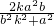 .根据|AB|=|AC|建立关于k、a、b的方程,化简整理得到(k-1)[b2k2+(b2-a2)k+b2]=0,结合题意得该方程有三个不相等的实数根,根据一元二次方程根与系数的关系和根的判别式建立关于a、b的不等式,解之即得c2>2b2,由此结合a2=b2+c2即可解出该椭圆的离心率的取值范围.
.根据|AB|=|AC|建立关于k、a、b的方程,化简整理得到(k-1)[b2k2+(b2-a2)k+b2]=0,结合题意得该方程有三个不相等的实数根,根据一元二次方程根与系数的关系和根的判别式建立关于a、b的不等式,解之即得c2>2b2,由此结合a2=b2+c2即可解出该椭圆的离心率的取值范围.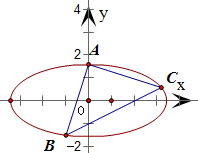 解:设椭圆的方程为
解:设椭圆的方程为 (a>b>0),
(a>b>0), x+b
x+b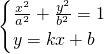 ,消去y并化简得(a2k2+b2)x2+2ka2bx=0
,消去y并化简得(a2k2+b2)x2+2ka2bx=0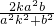 ,可得B的横坐标为-
,可得B的横坐标为-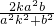 ,
, |x1-x2|=
|x1-x2|= •
•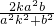 .
.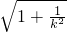 •
•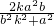
 •
•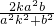 =
=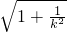 •
•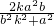 ,
, ,化简得c2>2b2
,化简得c2>2b2 >
> ,
, ,解之得e>
,解之得e> ,结合椭圆的离心率e<1,得
,结合椭圆的离心率e<1,得 <e<1
<e<1

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
已知三角形ABC的三个顶点均在椭圆![]() 上,且点A是椭圆短轴的一个端点(点A在y轴正半轴上).
上,且点A是椭圆短轴的一个端点(点A在y轴正半轴上).
若三角形ABC的重心是椭圆的右焦点,试求直线BC的方程;若角A为![]() ,AD垂直BC于D,试求点D的轨迹方程.
,AD垂直BC于D,试求点D的轨迹方程.
查看答案和解析>>
科目:高中数学 来源:2013年浙江省宁波市高考数学二模试卷(理科)(解析版) 题型:选择题
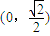
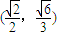
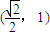
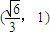
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com