Question

10．甲、乙两位学生参加数学竞赛培训，他们在培训期间8次模拟考试的成绩如下：
甲：82 81 79 78 95 88 93 84
乙：92 95 80 75 83 80 90 85
（1）画出甲、乙两位学生成绩的茎叶图，并求学生乙成绩的平均数和方差；
（2）从甲同学超过80分的6个成绩中任取两个，求这两个成绩中至少有一个超过90分的概率．

Answer 1

分析 （1）将成绩的十位数作为茎，个位数作为叶，可得茎叶图，计算乙的平均数与方差，即可求得结论，
（2）一一列举出任取两次成绩，所有基本事件，再找到满足两个成绩中至少有一个超过90分的基本事件，根据概率公式计算即可．

解答 解：（1）茎叶图如下：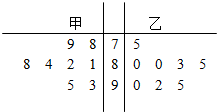
                               …（2分）
学生甲成绩中位数为83，…（3分）
（2）$\overline{x_乙}=\frac{1}{8}（75+80×2+83+85+90+92+95）$=85               …（4分）
S_乙²=$\frac{1}{8}$[（75-85）²+（80-85）²+（80-85）²+（83-85）²+（85-85）²+（90-85）²+（92-85）²+（95-85）²]=41                    …（6分）
（3）甲同学超过80（分）的成绩有82 81 95 88 93 84，
任取两次成绩，所有基本事件为：（82，81），（82，95），（82，88），（82，93），（82，84），（81，95），（81，88），（81，93），（81，84），（95，88），（95，93），（95，84），（88，93），（88，84），（93，84）共15个                               …（9分）
其中至少有一次超过90（分）的基本事件为：（82，95）（82，93）（81，95）（81，93）（95，88），（95，93），（95，84），（88，93）（93，84）共9个．          …（11分）
∴这两次成绩中至少有一次超过90（分）的概率为$\frac{9}{15}=\frac{3}{5}$．…（12分）

点评 本题考查茎叶图，考查平均数与方差的计算，考查概率公式，属于基础题．