
思路分析:设A(x1,y1),B(x2,y2),再设出直线的方程后将其与圆的方程联立.则所得方程组的解就是A和B的坐标值.但不必解出A和B坐标的具体的表达式,而要将目标放在利用根与系数关系表示出题目所给条件上.其中以AB为直径的圆可表示为(x-x1)(x-x2)+(y-y1)(y-y2)=0.
解:假设直线存在,设l的方程为y=x+m,
由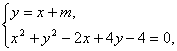
得2x2+2(m+1)x+m2+4m-4=0.(*)
设A(x1,y1),B(x2,y2),
则x1+y2=-(m+1),x1x2=![]() .
.
∵以AB为直径的圆(x-x1)(x-x2)+(y-y1)(y-y2)=0,
若它经过原点,则x1x2+y1y2=0.
又y1·y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2.
∴2x1x2+m(x1+x2)+m2=0,
∴m2+3m-4=0,m=-4或m=1.
∵当m=-4或m=1时,可验证(*)式的Δ>0,
∴所求直线l的方程是x-y-4=0或x-y+1=0.


科目:高中数学 来源: 题型:
(1)若点P(m,m+1)在圆C上,求直线PQ的斜率;?
(2)若M是圆上任一点,求|MQ|的最大值和最小值;
(3)若点N(a,b)满足关系式a2+b2![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程;
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
A.(-17,-7) B.(3,13)
C.(-17,-7)∪(3,13) D.[-17,-7]∪[3,13]
查看答案和解析>>
科目:高中数学 来源:2014届福建省福州市高一下学期期中数学试卷(解析版) 题型:填空题
已知圆C:x2+y2+2x+ay-3=0(a为实数)上任意一点关于直线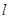 :x-y+2=0的对称点都在圆C上,则a=
.
:x-y+2=0的对称点都在圆C上,则a=
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com