
关于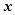 的函数
的函数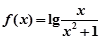 ,有下列结论:
,有下列结论:
①该函数的定义域是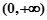 ;②该函数是奇函数;
;②该函数是奇函数;
③该函数的最小值为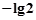 ;
④当
;
④当 时
时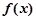 为增函数,当
为增函数,当 时
时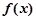 为减函数;
为减函数;
其中,所有正确结论的序号是
①④
【解析】
试题分析::①函数f(x)的定义域是(0,+∞),令 >0,解得x>0,故定义域是(0,+∞),命题正确;
>0,解得x>0,故定义域是(0,+∞),命题正确;
②函数f(x)是奇函数,由①知,定义域不关于原点对称,故不是奇函数,命题不正确;
③函数f(x)的最小值为-lg2,因为f(x)=lg =lg
=lg ≤lg
≤lg =-lg2,最大值是-lg2,故命题不正确;
=-lg2,最大值是-lg2,故命题不正确;
④当0<x<1时,函数f(x)是增函数;当x>1时,函数f(x)是减函数,命题正确,因为f′(x)=lg ,令导数大于0,可解得0<x<1,令导数大于0,得x>1,故命题正确.综上,①④正确
,令导数大于0,可解得0<x<1,令导数大于0,得x>1,故命题正确.综上,①④正确
考点:本试题主要考查了函数定义域、最值、单调性和奇偶性,同时考查了推理论证的能力以及计算论证的能力,属于中档题.
点评:解决该试题的关键是①根据对数函数的真数大于0,建立关系式解之验证定义域即可;②函数f(x)是奇函数,利用奇函数的定义进行判断;③函数f(x)的最小值为-lg2,利用基本不等式与对数的运算性质求出最值;④求出导数,解出单调区间,验证即可.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源:2012-2013学年山东省高三第二次(3月)周测理科数学试卷(解析版) 题型:填空题
关于函数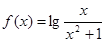 ,有下列结论:①函数
,有下列结论:①函数 的定义域是(0,+∞);②函数
的定义域是(0,+∞);②函数 是奇函数;③函数
是奇函数;③函数 的最小值为-
的最小值为-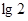 ;④当
;④当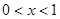 时,函数
时,函数 是增函数;当
是增函数;当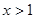 时,函数
时,函数 是减函数.
是减函数.
其中正确结论的序号是 .(写出所有你认为正确的结论的序号)
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省偃师市高一第三次月考数学试卷(解析版) 题型:填空题
关于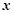 的函数
的函数 ,有下列结论:
,有下列结论:
①、该函数的定义域是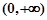 ;
;
②、该函数是奇函数;
③、该函数的最小值为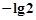 ;
;
④、当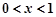 时
时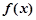 为增函数,当
为增函数,当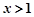 时
时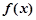 为减函数;
为减函数;
其中,所有正确结论的序号是 。
查看答案和解析>>
科目:高中数学 来源:2015届湖北武汉部分重点中学高一上期中考试数学试卷(解析版) 题型:填空题
关于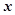 的函数
的函数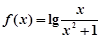 ,有下列结论:
,有下列结论:
①、该函数的定义域是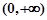 ; ②、该函数是奇函数;
; ②、该函数是奇函数;
③、该函数的最小值为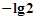 ;
;
④、当 时
时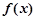 为增函数,当
为增函数,当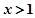 时
时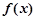 为减函数;
为减函数;
其中,所有正确结论的序号是 。
查看答案和解析>>
科目:高中数学 来源:2010年江苏省高一第一学期期中考试数学卷 题型:填空题
对于给定的函数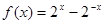 ,有下列四个结论:
,有下列四个结论:
①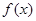 的图象关于原点对称;
②
的图象关于原点对称;
②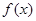 在R上是增函数;
在R上是增函数;
③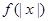 的图象关于
的图象关于 轴对称; ④
轴对称; ④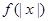 的最小值为0;
的最小值为0;
其中正确的是 ★ (填写正确的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com