
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
分析 根据向量夹角余弦的坐标公式可以求出$cos<\overrightarrow{a},\overrightarrow{b}>$,从而根据向量夹角的范围便可得出$<\overrightarrow{a},\overrightarrow{b}>$.
解答 解:$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{-3\sqrt{3}+\sqrt{3}}{2•\sqrt{12}}$=$-\frac{1}{2}$;
∴$<\overrightarrow{a},\overrightarrow{b}>=\frac{2π}{3}$.
故:选D.
点评 考查向量数量积的坐标运算,向量夹角余弦的坐标公式,清楚向量夹角的范围,以及已知三角函数值求角.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0° | B. | 60° | C. | 90° | D. | 180° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
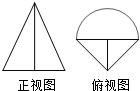 由两个简单几何体构成的组合几何体的三视图中,正视图和俯视图如右图所示,其中正视图中等腰三角形的高为3,俯视图中的三角形均为等腰直角三角形,半圆直径为2,则该几何体的体积为( )
由两个简单几何体构成的组合几何体的三视图中,正视图和俯视图如右图所示,其中正视图中等腰三角形的高为3,俯视图中的三角形均为等腰直角三角形,半圆直径为2,则该几何体的体积为( )| A. | $\frac{π}{2}+1$ | B. | π+1 | C. | $\frac{π}{2}+3$ | D. | π+3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com