练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设三棱柱的侧棱垂直于底面，所有棱的长都为3，顶点都在一个球面上，则该球的表面积为________．

    21π
    分析：由题意可知上下底面中心连线的中点就是球心，求出球的半径，即可求出球的表面积．
    解答：根据题意条件可知三棱柱是棱长都为3的正三棱柱，
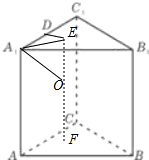
    设上下底面中心连线EF的中点O，则O就是球心，其外接球的半径为OA1，
    又设D为A1C1中点，在直角三角形EDA1中，EA1==
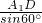
    在直角三角形OEA1中，OE=，由勾股定理得OA1=
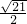
    ∴球的表面积为S=4π•=21π，
    故答案为：21π．
    点评：本题考查空间几何体中位置关系、球和正棱柱的性质以及相应的运算能力和空间形象能力．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设三棱柱的侧棱垂直于底面，所有棱长都为a，顶点都在一个球面上，则该球的表面积为（　　）
    A、πa2
    B、
    7
    3
    πa2
    C、
    11
    3
    πa2
    D、5πa2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设三棱柱的侧棱垂直于底面，所有棱的长都为a，顶点都在一个球面上，则该球的表面积为
    7
    3
    πa2
    7
    3
    πa2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•眉山二模）设三棱柱的侧棱垂直于底面，所有棱的长都为3，顶点都在一个球面上，则该球的表面积为
    21π
    21π
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设三棱柱的侧棱垂直于底面，所有棱长都为，顶点都在一个球面上，则该球的表面积为

    (A)        (B)            (C)   (D)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设三棱柱的侧棱垂直于底面，所有棱长都为，顶点都在一个球面上，则该球的表面积为

    (A)        (B)            (C)   (D)

    查看答案和解析>>

    同步练习册答案