Question

求证两两相交而不过同一点的四条直线必在同一个平面内．

Answer 1

【答案】分析：解决此题，先要画出图形，前三条线只能画成“两两相交，且不交于同一点”，这样才能保证第四条线与前三条全相交，这样的话图形一共可以分为两类．然后，我们可以根据推论1或者推论2，先把平面确定好，然后再根据公理1，进一步证明其余的直线也在这个平面里．
解答：证明：第一种情形（如图1）：四条直线l₁，l₂，l₃，l₄没有三条直线过同一点，
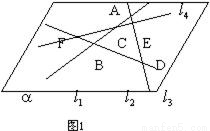
这时它们共有六个交点A、B、C、D、E、F，它们各不相同，
因直线l₁，l₂相交于点A，可决定一平面α；
因点B、C、D、E均在平面α内，
所以直线l₃，l₄也在平面α内，
故直线l₁，l₂，l₃，l₄同在平面α内．

第二种情形（如图2）：四条直线l₁，l₂，l₃，l₄中有三条，
例如l₁，l₂，l₃，过同一点A，
因直线l₄不过点A，
故由点A及直线l₄可决定一平面α，
因直线l₄与直线l₁，l₂，l₃，相交，
设交点为B、C、D，
则点B、C、D在直线l₄上，从而在平面α内，
因此，直线l₁，l₂，l₃，各有两点在平面α内，
即这三条直线在平面α内，
故四直线l₁，l₂，l₃，l₄在同一平内．
点评：此题难度系数不大，关键在于画对图形．重点考查了推论1、2与公理1，这些都是很简单的道理，但是能够运用起来，却不是那么容易，做题时不要烦躁，理清线条，定理运用其实很简单!