
(09年湖南十二校文)(13分)
![]() 设函数
设函数![]() (
(![]() >0)
>0)
![]() (Ⅰ)若
(Ⅰ)若![]() 在
在![]() 时,有极值
时,有极值![]() ,求
,求![]() 的单调区间。
的单调区间。
![]() (Ⅱ)证明:
(Ⅱ)证明:![]() 的图像上存在着与直线
的图像上存在着与直线![]() 垂直的切线。
垂直的切线。
解析:(Ⅰ)![]()
![]() 由题意可知
由题意可知 即
即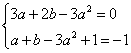 ……………1分
……………1分
![]() 解得
解得 ![]() 舍去) ………………2分
舍去) ………………2分
![]() 此时,
此时,![]()
![]() 令
令![]() >0得
>0得![]() >1或
>1或![]() <
<![]() 1
1
![]()
![]() <0得
<0得 ![]() 1<
1<![]() <1 ………………………3分
<1 ………………………3分
![]() 所以
所以![]() 的递增区间为(
的递增区间为(![]() ∞,
∞,![]() 1)、(1,+∞)
1)、(1,+∞)
![]() 递减区间为(
递减区间为(![]() 1,1) ………………………4分
1,1) ………………………4分
![]() (Ⅱ)证明:①当
(Ⅱ)证明:①当![]() 时,直线
时,直线![]() ,则
,则![]() 图像上与
图像上与![]() 垂直的切线斜率为0.
垂直的切线斜率为0.
![]() 令
令![]() >0恒成立,方程有解。 …………5分
>0恒成立,方程有解。 …………5分
![]()
![]() ②当
②当![]()
![]() 时,直线
时,直线![]() 的斜率为
的斜率为![]() ,则与
,则与![]() 垂直的切线斜率为
垂直的切线斜率为![]()
![]() 令
令![]() 即
即![]()
![]()
![]() >0恒成立,方程有解。
>0恒成立,方程有解。
![]() 综上所述:
综上所述:![]() 的图像上存在着与
的图像上存在着与![]() 垂直的直线。 ……………7分
垂直的直线。 ……………7分
![]() (Ⅲ)由题意可知,
(Ⅲ)由题意可知,![]() 为
为![]() 的两根
的两根
![]()
![]() ………8分
………8分
![]() 从而
从而![]()
![]() ……………………………9分
……………………………9分
![]() 由
由![]() 得 0<
得 0<![]() …………………………………10分
…………………………………10分
![]() 设
设![]()
![]()
![]()
![]() 令
令![]() 则
则![]() ……………………………………11分
……………………………………11分
![]() 故
故![]() 在
在![]() 递增,
递增,![]() 递减, 从而
递减, 从而![]() 在
在![]() 上的极大值为
上的极大值为![]()
![]() 即最大值为
即最大值为![]() ,且最小值为0,则
,且最小值为0,则![]()
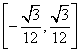 …………………………13分
…………………………13分 

科目:高中数学 来源: 题型:
(09年湖南十二校文)(13分)
![]() 对于数列
对于数列![]() 定义数列
定义数列![]() 为
为![]() 的“和数列”
的“和数列”
![]() (1)若
(1)若![]() 的“和数列”的通项为2n+1,
的“和数列”的通项为2n+1,![]() ,求
,求![]() ,并写出
,并写出![]() 的通项公式。(不必证明)
的通项公式。(不必证明)
![]() (2)若
(2)若![]() 的“和数列”的通项为
的“和数列”的通项为![]() ,数列
,数列![]() 满足
满足![]() ,求
,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年湖南十二校文)(12分)某高等学校自愿献血的50位学生的血型分布的情况如下表:
![]()
血型 | A | B | AB | O |
人数 | 20 | 10 | 5 | 15 |
![]() (Ⅰ)从这50位学生中随机选出2人,求这2人血型都为A型的概率;
(Ⅰ)从这50位学生中随机选出2人,求这2人血型都为A型的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年湖南十二校文)对于区间![]() 上有意义的两个函数
上有意义的两个函数![]() 与
与![]() ,如果对于区间
,如果对于区间![]() 中的任意数
中的任意数![]() 均有
均有![]() ,则称函数
,则称函数![]() 与
与![]() 在区间
在区间![]() 上是密切函数,
上是密切函数,![]() 称为密切区间.若
称为密切区间.若![]() 与
与![]() 在某个区间上是“密切函数”,则它的一个密切区间可能是( )
在某个区间上是“密切函数”,则它的一个密切区间可能是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com