
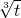 .水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选择为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出?
.水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选择为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出?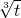 ,且0≤t≤16.
,且0≤t≤16.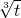 ≤300.
≤300. )
)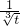 ,由0<t≤16,m≥
,由0<t≤16,m≥ ,
, )=1+10m2-10m3,(m≥
)=1+10m2-10m3,(m≥ ),
), .
. ≤m<
≤m< 时,f′(t)>0;当m>
时,f′(t)>0;当m> 时,f′(t)<0,
时,f′(t)<0, 时(此时t=
时(此时t=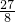 ),f(t)最大值=1+10(
),f(t)最大值=1+10( )2-10(
)2-10( )3=
)3= ≈2.48.
≈2.48.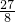 时,1+10(
时,1+10( )有最大值2.48.∴x>2.48,即x≥3.
)有最大值2.48.∴x>2.48,即x≥3. +1,
+1, +1取最小值
+1取最小值 +1=
+1= ∈(3,4).
∈(3,4).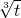 ,且0≤t≤16.解0<y≤300,当t>0时,由左边得x>1+10(
,且0≤t≤16.解0<y≤300,当t>0时,由左边得x>1+10( ).再令m=
).再令m=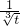 ,以m为单位得到函数y=1+10m2-10m3,(m≥
,以m为单位得到函数y=1+10m2-10m3,(m≥ ),利用导数讨论这个函数的单调性,得出x≥3,再由右边得x≤
),利用导数讨论这个函数的单调性,得出x≥3,再由右边得x≤ +1,类似于前面的讨论得出x≤3,从而最终得出x=3.
+1,类似于前面的讨论得出x≤3,从而最终得出x=3.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、x=2,n=24 | B、x=16,n=24ks**5u | C、x=2,n=80 | D、x=16,n=80 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com