
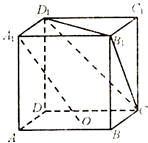
 已知点O为正方体ABCD-A1B1C1D1底面ABCD的中心,则下列结论正确的是
已知点O为正方体ABCD-A1B1C1D1底面ABCD的中心,则下列结论正确的是 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
 (甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=2
(甲)如图,已知斜三棱柱ABC-A1B1C1的侧面A1C⊥底面ABC,∠ABC=90°,BC=2,AC=2| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河南省安阳三中高三(上)第二次月考数学试卷(文科)(解析版) 题型:填空题
 的正方体ABCD-A1B1C1D1,它的外接球的球心为O,点E是AB的中点,点P是球O的球面上任意一点,有以下判断:①该正方体外接球的体积是36π;②异面直线OE与B1C所成角为90°;③PE长的最大值为
的正方体ABCD-A1B1C1D1,它的外接球的球心为O,点E是AB的中点,点P是球O的球面上任意一点,有以下判断:①该正方体外接球的体积是36π;②异面直线OE与B1C所成角为90°;③PE长的最大值为 ;④过点E的平面截球O的截面面积的最小值为6π.其中所有正确判断的序号是 .
;④过点E的平面截球O的截面面积的最小值为6π.其中所有正确判断的序号是 .查看答案和解析>>
科目:高中数学 来源:2010年新教材高考数学模拟题详解精编试卷(8)(解析版) 题型:解答题
 ,又AA1⊥A1C,AA1=A1C.
,又AA1⊥A1C,AA1=A1C.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com