设p:a2-a<0.q:当x∈[1,2]时,x2-x-4a≤0恒成立.如果p∨q为真命题,p∧q为假命题,求a的范围.
【答案】
分析:可在p真的基础上求得a的范围,同理在q真的基础上求得a的范围,再由“p∨q为真命题,p∧q为假命题”可得p与q有且只有一个为真命题,分类讨论即可.
解答:解:对于p:∵a
2-a<0
∴0<a<1.
设f(x)=x
2-x-4a,x∈[1,2].
其对称轴
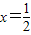
,故f(x)在[1,2]上单调递增,
∴f(x)
max=f(2)=2-4a.
由x∈[1,2]时,x
2-x-4a≤0恒成立,得2-4a≤0,即
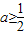
.
因为p∨q为真命题,p∧q为假命题,所以p与q有且只有一个为真命题.
如果p真且q假,则
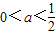
;
如果p假且q真,则a≥1.
所以a的取值范围为(0,

)∪[1,+∞).
点评:本题考查二次函数在闭区间上的最值,着重考查复合命题的真假的判断,难点在于对“x∈[1,2]时,x
2-x-4a≤0恒成立”的理解与应用,突出考查化归思想与分类讨论思想,属于中档题.

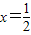 ,故f(x)在[1,2]上单调递增,
,故f(x)在[1,2]上单调递增,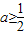 .
.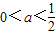 ;
; )∪[1,+∞).
)∪[1,+∞).
