练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知数列，，

    （Ⅰ）当为何值时，数列可以构成公差不为零的等差数列,并求其通项公式；

    （Ⅱ）若，令,求数列的前项和。

    解:  1）

    --------1分

             

        得    -----------------3分

        当 时,       不合题意舍去-----------4分

    时,带入可得: ---------------------------5分

       构成以为首项,公差为 -1 的等差数列;------------ ----6分

    2）由 可得,,

    就有,-------------------------------------------------．8分

    即,,又构成以为首项,公比为3 的等比数列;

       ----------10分 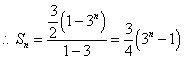  -----------12分

       （若由时,直接得: ;即时,恒成立,

        构成以为首项,公差为1 的等差数列;  www.k@s@5@u.com                            高#考#资#源#网

    则． ………该解法不严谨本小题扣2分）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知数列an是首项为1的等比数列，Sn是an的前n项和，且S6=9S3，则数列an的通项公式是（　　）
    A、2n-1B、21-nC、31-nD、3n-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列an的前n项和为Sn，a1=2，nan+1=Sn+n（n+1），
    （1）求数列an的通项公式；
    （2）设bn=
    Sn2n
    ，如果对一切正整数n都有bn≤t，求t的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列an满足a1=1，an+1=an+n（n∈N*），数列bn满足b1=1，（n+2）bn+1=nbn（n∈N*），数列cn满足c1=1，
    c1
    1
    +
    c2
    22
    +…+
    cn
    n2
    =
    cn+1
    n+1
    （n∈N*）
    （1）求数列{an}、{bn}的通项公式；
    （2）求数列cn的通项公式；
    （3）是否存在正整数k使得k(an+
    7
    2
    )-
    3
    bn+1
    ＞cn+6n+15    对一切n∈N*恒成立，若存在求k的最小值；若不存在请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设数列{an}的前n项和为Sn，Tn=
    S1+S2+…+Sn
    n
    ，称Tn为数列a1，a2，…an的“理想数”，已知数列a1，a2，…a500的“理想数”为2004，那么数列2，a1，a2，…a500的“理想数”为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列
    		2
    、
    		6
    、
    		10
    、
    		14
    、3
    		2
    …那么7
    		2
    是这个数列的第几项（　　）
    A、23B、24C、19D、25

    查看答案和解析>>

    同步练习册答案