
分析 ①抛物线x2=4y的焦点在y轴上,判断原命题错误;
②等差数列{an}为常数列时,公比q=1,判断原命题错误;
③利用基本不等式求出$\frac{2}{a}+\frac{3}{b}$的最小值为$5+2\sqrt{6}$,判断原命题正确;
④由正弦定理得出$\frac{sinA}{cosA}$=$\frac{sinB}{cosB}$=$\frac{sinC}{cosC}$,A=B=C=60°判断原命题正确.
解答 解:对于①,抛物线x2=4y的焦点坐标是(0,1),原命题错误;
对于②,等差数列{an}中,a1,a3,a4成等比数列,则${{(a}_{1}+2d)}^{2}$=a1(a1+3d),
当d=0时,a1=a3=a4,公比q=1;
当d≠0时,a1=-4d,a3=-2d,a4=-d,公比q=$\frac{1}{2}$;原命题错误;
对于③,a>0,b>0,a+b=1,则
$\frac{2}{a}+\frac{3}{b}$=$\frac{2a+2b}{a}$+$\frac{3a+3b}{b}$=5+$\frac{2b}{a}$+$\frac{3a}{b}$≥5+2$\sqrt{6}$,当且仅当$\frac{2b}{a}$=$\frac{3a}{b}$时“=”成立;
即最小值为$5+2\sqrt{6}$,原命题正确;
对于④,△ABC中,$\frac{a}{cosA}=\frac{b}{cosB}=\frac{c}{cosC}$,
由正弦定理得$\frac{sinA}{cosA}$=$\frac{sinB}{cosB}$=$\frac{sinC}{cosC}$,
即tanA=tanB=tanC;
又A、B、C∈(0,π),
所以A=B=C=60°;原命题正确;
综上,正确的命题序号是③④.
故答案为:③④.
点评 本题考查了命题真假的判断问题,也考查了抛物线与等差、等比数列的应用问题,基本不等式与解三角形的应用问题,是综合性题目.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 《算法统宗》是中国古代数学名著,由明代数学家程大位编著.《算法统宗》对我国民间普及珠算和数学知识起到了很大的作用,是东方古代数学的名著.在这部著作中,许多数学问题都是以歌诀形式呈现的,“竹筒容米”就是其中一首:家有九節竹一莖,為因盛米不均平;下頭三節三升九,上梢四節貯三升;唯有中間二節竹,要將米數次第盛;若是先生能算法,也教算得到天明!大意是:用一根9节长的竹子盛米,每节竹筒盛米的容积是不均匀的.下端3节可盛米3.9升,上端4节可盛米3升.要按依次盛米容积相差同一数量的方式盛米,中间两节可盛米多少升?由以上条件,计算出中间两节的容积为( )
《算法统宗》是中国古代数学名著,由明代数学家程大位编著.《算法统宗》对我国民间普及珠算和数学知识起到了很大的作用,是东方古代数学的名著.在这部著作中,许多数学问题都是以歌诀形式呈现的,“竹筒容米”就是其中一首:家有九節竹一莖,為因盛米不均平;下頭三節三升九,上梢四節貯三升;唯有中間二節竹,要將米數次第盛;若是先生能算法,也教算得到天明!大意是:用一根9节长的竹子盛米,每节竹筒盛米的容积是不均匀的.下端3节可盛米3.9升,上端4节可盛米3升.要按依次盛米容积相差同一数量的方式盛米,中间两节可盛米多少升?由以上条件,计算出中间两节的容积为( )| A. | 2.1升 | B. | 2.2升 | C. | 2.3升 | D. | 2.4升 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x+2y-1=0 | B. | 3x+2y-7=0 | C. | 2x-3y+5=0 | D. | 2x-3y+8=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-1,\frac{1}{2}}]$ | B. | $[{-2,\frac{1}{2}}]$ | C. | [-1,0] | D. | [-2,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
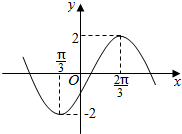 已知函数f(x)=Asin(ωx+φ)(其中A,ω,φ为常数,且A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示:
已知函数f(x)=Asin(ωx+φ)(其中A,ω,φ为常数,且A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com