按下列要求分配6本不同的书,各有多少种不同的分配方式?
(1)分成三份,1份1本,1份2本,1份3本;
(2)甲、乙、丙三人中,一人得1本,一人得2本,一人得3本;
(3)平均分成三份,每份2本.
解:(1)无序不均匀分组问题.先选1本有C
16种选法;再从余下的5本中选2本有C
25种选法;最后余下3本全选有C
33种方法,故共有C
16C
25C
33=60种.
(2)有序不均匀分组问题.由于甲、乙、丙是不同的三人,在第(1)题基础上,还应考虑再分配,共有C
16C
25C
33A
33=360种.
(3)无序均匀分组问题.先分三步,则应是C
26C
24C
22种方法,但是这里出现了重复.不妨记6本书为A、B、C、D、E、F,若第一步取了AB,第二步取了CD,第三步取了EF,记该种分法为(AB,CD,EF),则C
26C
24C
22种分法中还有(AB,EF,CD)、(CD,AB,EF)、(CD,EF,AB)、(EF,CD,AB)、(EF,AB,CD),共A
33种情况,而这A
33种情况仅是AB、CD、EF的顺序不同,因此只能作为一种分法,故分配方式有
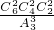
=15种.
分析:(1)分成三份,1份1本,1份2本,1份3本,是无序不均匀分组问题,直接利用组合数公式求解即可.
(2)甲、乙、丙三人中,一人得1本,一人得2本,一人得3本,甲、乙、丙三人有序不均匀分组问题.直接就是即可.
(3)平均分成三份,每份2本.这是平均分组问题,列举(AB,CD,EF),(AB,EF,CD)、(CD,AB,EF)、(CD,EF,AB)、(EF,CD,AB)、(EF,AB,CD)是一种分法,求出组合总数除以A
33即可.
点评:本题考查排列、组合及简单计数问题,正确区分无序不均匀分组问题.有序不均匀分组问题.无序均匀分组问题.是解好组合问题的一部分;本题考查计算能力,理解能力.

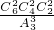 =15种.
=15种.

 阅读快车系列答案
阅读快车系列答案