练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本题满分13分）的三个内角依次成等差数列．

       （Ⅰ）若，试判断的形状；

       （Ⅱ）若为钝角三角形，且，求

    的取值范围．

     

    【答案】

    （1）为正三角形；（2）.

    【解析】本试题主要是考查了解三角形的运用，以及数列的性质的综合运用。

    第一问中，利用的三个内角依次成等差数列．得到角B，然后利用得到，结合余弦定理得到a=c,然后判定形状即可

    第二问中，因为为钝角三角形，且，那么则可以由=化简为f(A)=

    利用角A的范围求解值域。

    解：（Ⅰ）∵，   ∴ .  ∵依次成等差数列，

    ∴,.    由余弦定理，

    ，∴.  ∴为正三角形……………………6分

    （Ⅱ）=

         ===……10分

    ∵,         ∴，        ………………11分

    ∴ ，   

    ∴的取值范围是……13分

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （本题满分13分）

             如图，两个圆形转盘A，B，每个转盘阴影部分各占转盘面积的。某“幸运转盘积分活动”规定，当指针指到A，B转盘阴影部分时，分别赢得积分1000分和2000分。先转哪个转盘由参与者选择，若第一次赢得积分，可继续转为另一个转盘，此时活动结束，若第一次未赢得积分，则终止活动。

       （1）记先转A转盘最终所得积分为随机量X，则X的取值分别是多少？

       （2）如果你参加此活动，为了赢得更多的积分，你将选择先转哪个转盘？请说明理由。

    查看答案和解析>>

    科目：高中数学 来源：2014届福建省高二上学期第一次月考理科数学试卷（解析版） 题型：解答题

    (本题满分13分)  已知关于x的二次函数

    （1）设集合和，从集合中随机取一个数作为，从中随机取一个数作为，求函数在区间上是增函数的概率；

    （2）设点是区域内的随机点，求函数在区间上是增函数的概率.

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年福建省漳州市四地七校高三第四次联考理科数学试卷（解析版） 题型：解答题

    （本题满分13分）如图，在三棱柱中，已知

    侧面

    (Ⅰ)求直线C1B与底面ABC所成角正切值；

    (Ⅱ)在棱（不包含端点上确定一点的位置，使得(要求说明理由).

    (Ⅲ)在（2）的条件下,若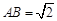，求二面角的大小.

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年北京市朝阳区高三上学期期末考试理科数学 题型：解答题

    （本题满分13分）

    在锐角中，，，分别为内角，，所对的边，且满足．

    （Ⅰ）求角的大小；

    （Ⅱ）若，且，，求的值．

     

    查看答案和解析>>

    同步练习册答案