
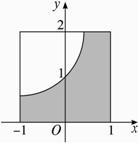
图3-3-21
【探究】在坐标系中画出正方形,用随机模拟的方法可以求出图3321中阴影部分面积与正方形面积之比,从而求得阴影部分面积的近似值.
【解析】(1)利用计算机产生两组[0,1]上的均匀随机数,a1=RAND,b1=RAND.
(2)进行平移或伸缩变换,a=2a1-1,b=b1*2,得到一组[-1,1]上的均匀随机数和一组[0,2]上的均匀随机数.
(3)统计试验总次数N和落在阴影内的次数N1(满足条件b<2a的点(a,b)).
(4)计算频率![]() ,即为点落在阴影部分的概率的近似值.
,即为点落在阴影部分的概率的近似值.
(5)用几何概率公式求得点落在阴影部分的概率为
P=![]() .∴
.∴![]() ≈
≈![]() .∴S≈
.∴S≈![]() 即为阴影部分面积的近似值.
即为阴影部分面积的近似值.
规律总结 解决本题的关键是利用随机模拟法和几何概率公式分别求得几何概率,然后通过方程求得阴影部分面积的近似值.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011年湖北省黄冈市黄州一中高考数学模拟试卷(二)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省高三第十次模拟考试理科数学试卷(解析版) 题型:选择题
下图的程序框图中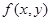 是产生随机数的函数,它能随机产生区间
是产生随机数的函数,它能随机产生区间 内的任何一个数,如果输入N值为4000,输出的m值为1840,则利用随机模拟方法计算由
内的任何一个数,如果输入N值为4000,输出的m值为1840,则利用随机模拟方法计算由
 与
与 及
及 轴所围成面积的近似值为( )
轴所围成面积的近似值为( )

A.0.46 B.2.16 C.1.84 D.0.54
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com