
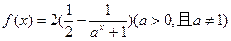 .
.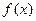 的反函数解析式;
的反函数解析式;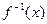 的奇偶性;
的奇偶性;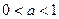 时,
时, 解不定式
解不定式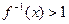 .
.科目:高中数学 来源:不详 题型:解答题
 术知识,该鱼塘中鱼的总量不能超过19.5(万条)(不考虑鱼的自然繁殖和死亡等因素对鱼总量的影响),所以该鱼塘采取对放入鱼塘的新鱼数进行控制,该鱼塘每年只放入新鱼
术知识,该鱼塘中鱼的总量不能超过19.5(万条)(不考虑鱼的自然繁殖和死亡等因素对鱼总量的影响),所以该鱼塘采取对放入鱼塘的新鱼数进行控制,该鱼塘每年只放入新鱼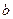 (万条).
(万条).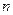 年年初该鱼塘的鱼总量为
年年初该鱼塘的鱼总量为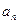 (年初已放入新鱼
(年初已放入新鱼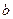 (万条),2010年为第一年),求
(万条),2010年为第一年),求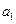 及
及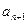 与
与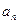 间的关系;
间的关系;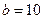 时,试问能否有效控制鱼塘总量不超过19.5(万条)?若有效,说明理由;若无效,请指出哪一年初开始鱼塘中鱼的总量超过19.5(万条).
时,试问能否有效控制鱼塘总量不超过19.5(万条)?若有效,说明理由;若无效,请指出哪一年初开始鱼塘中鱼的总量超过19.5(万条).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com