
如图C,D是以AB为直径的圆上的两点, ,F是AB上的一点,且
,F是AB上的一点,且 ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知


(1)求证:AD 平面BCE
平面BCE
(2)求证:AD//平面CEF;
(3)求三棱锥A-CFD的体积.
(1)参考解析;(2)参考解析;(3) 
【解析】
试题分析:(1)因为由于AB是圆的直径,所以AD⊥BD,又因为点C在平面ABD的射影E在BD上,所以CE⊥平面ADB.又因为 平面ADB.所以AD⊥CE.又因为
平面ADB.所以AD⊥CE.又因为 .所以AD⊥平面BCE.
.所以AD⊥平面BCE.
(2)因为 ,
,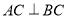 .有直角三角形的勾股定理可得
.有直角三角形的勾股定理可得 .在直角三角形BCE中,又
.在直角三角形BCE中,又 .所以
.所以 .又BD=3,
.又BD=3, .所以可得
.所以可得 .所以AD∥FE,又因为
.所以AD∥FE,又因为 平面CEF,
平面CEF, 平面CE.所以AD//平面CEF.
平面CE.所以AD//平面CEF.
(3)通过转换顶点三棱锥A-CFD的体积 .因为
.因为
 .所以
.所以 .
.
试题解析:(1)证明:依题意:


 平面
平面 ∴
∴



 ∴
∴ 平面
平面 . 4分
. 4分
(2)证明: 中,
中, ,
, ∴
∴
 中,
中, ,
, ∴
∴ .
.
∴ . ∴
. ∴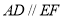

 在平面
在平面 外,
外, 在平面
在平面 内,
内,
∴ 平面
平面 . 8分
. 8分
(3)【解析】
由(2)知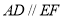 ,
,
 ,且
,且

 平面
平面
∴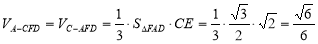 . 12分
. 12分
考点:1.线面垂直.2.线面平行.3.几何体的体积公式.4.图形的翻折问题.


科目:高中数学 来源:2016届辽宁省高一下学期期初入学考试数学试卷(解析版) 题型:选择题
下列四个命题中正确的是( )
①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.
A. ①和② B. ②和③ C. ③和④ D. ②和④
查看答案和解析>>
科目:高中数学 来源:2016届辽宁省五校高一上学期期末联考数学试卷(解析版) 题型:选择题
设 是x轴上的不同两点,点P的横坐标为2,|PA|=|PB|,若直线PA的方程为
是x轴上的不同两点,点P的横坐标为2,|PA|=|PB|,若直线PA的方程为 ,则直线PB的方程是( )
,则直线PB的方程是( )
(A) (B)
(B)  (C)
(C)  (D)
(D) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com