
(1)y=2x-lnx;
(2)y=![]() +cosx;
+cosx;
(3)y=x3-x.
解:(1)函数的定义域为(0,+∞),
其导数f′(x)=2-![]() .
.
令2-![]() >0,解得x>
>0,解得x>![]() .
.
令2-![]() <0,解得0<x<
<0,解得0<x<![]() .
.
因此(![]() ,+∞)为该函数的单调增区间,(0,
,+∞)为该函数的单调增区间,(0,![]() )为该函数的单调减区间.
)为该函数的单调减区间.
(2)函数的定义域为R.
f′(x)=![]() -sinx.
-sinx.
令![]() -sinx>0,解得2kπ-
-sinx>0,解得2kπ-![]() π<x<2kπ+
π<x<2kπ+![]() (k∈Z).
(k∈Z).
令![]() -sinx<0,解得2kπ+
-sinx<0,解得2kπ+![]() <x<2kπ+
<x<2kπ+![]() π(k∈Z).
π(k∈Z).
因此f(x)在(2kπ+![]() ,2kπ+
,2kπ+![]() )(k∈Z)上为减函数,在(2kπ-
)(k∈Z)上为减函数,在(2kπ-![]() ,2kπ+
,2kπ+![]() )(k∈Z)上为增函数.
)(k∈Z)上为增函数.
(3)函数的定义域为R.
令y′=3x2-1>0,得x<-![]() 或x>
或x>![]() .
.
令y′=3x2-1<0,得-![]() <x<
<x<![]() .
.
∴y=x3-x有三个单调区间,其中在(-∞,-![]() )及(
)及(![]() ,+∞)上是增函数,在(-
,+∞)上是增函数,在(-![]() ,
,![]() )上为减函数.
)上为减函数.
点评:(1)研究函数单调性的程序是:先确定其定义域,再求导,最后通过f′(x)>0与f′(x)<0来求出其单调区间.
(2)(3)题中增区间有两个,但不能取并集.
(3)(2)题中符号(2kπ+![]() ,2kπ+
,2kπ+![]() )(k∈Z)表示若干个单调区间,不表示并集,它相当于(
)(k∈Z)表示若干个单调区间,不表示并集,它相当于(![]() ,
,![]() )、(
)、(![]() ,
,![]() )、….
)、….


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源:2012年人教A版高中数学必修四1.4三角函数的图像与性质练习卷(四)(解析版) 题型:解答题
求下列函数的单调区间:
(1)y=tan ; (2)y=
; (2)y= tan2x+1;
tan2x+1;
(3)y=3tan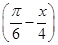 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com