【答案】
分析:本题可用分析法来解答,分析法:证明使x
4+y
4≥
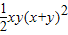
成立的充分条件成立,
解答:证明:要证x
4+y
4≥
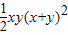
,只需证明2(x
4+y
4)≥xy(x+y)
2,
即证2(x
4+y
4)≥x
3y+xy
3+2x
2y
2,---------------------------(4分)
只需x
4+y
4≥x
3y+xy
3与x
4+y
4≥2x
2y
2同时成立即可,
又知x
4+y
4-2x
2y
2=(x
2-y
2)
2≥0,即x
4+y
4≥2x
2y
2成立,
只需再有x
4+y
4≥x
3y+xy
3成立即可,--------------------(8分)
由于x
4+y
4-x
3y-xy
3=(x-y)(x
3-y
3)
∵x-y与x
3-y
3同号,∴(x-y)(x
3-y
3)≥0,即x
4+y
4≥x
3y+xy
3成立,
∴对于任意实数x,y都有x
4+y
4≥

成立--------------(12分)
点评:本小题主要考查不等式的证明等基础知识,考查运算变形能力,考查化归与转化思想.属于基础题.

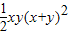 .
.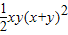 成立的充分条件成立,
成立的充分条件成立,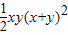 ,只需证明2(x4+y4)≥xy(x+y)2,
,只需证明2(x4+y4)≥xy(x+y)2, 成立--------------(12分)
成立--------------(12分)
