
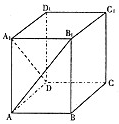
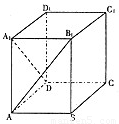
 如图,在高为4的长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,则直线AB1与DA1所成角的余弦值是
如图,在高为4的长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,则直线AB1与DA1所成角的余弦值是



 ,AC=2
,AC=2
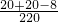 =
=


科目:高中数学 来源: 题型:
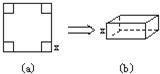 有一块边长为4的正方形钢板,现对其进行切割、焊接成一个长方体形无盖容器(切、焊损耗忽略不计).有人应用数学知识作了如下设计:如图(a),在钢板的四个角处各切去一个小正方形,剩余部分围成一个长方体,该长方体的高为小正方形边长,如图(b).
有一块边长为4的正方形钢板,现对其进行切割、焊接成一个长方体形无盖容器(切、焊损耗忽略不计).有人应用数学知识作了如下设计:如图(a),在钢板的四个角处各切去一个小正方形,剩余部分围成一个长方体,该长方体的高为小正方形边长,如图(b).查看答案和解析>>
科目:高中数学 来源: 题型:
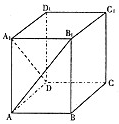 如图,在高为4的长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,则直线AB1与DA1所成角的余弦值是( )
如图,在高为4的长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,则直线AB1与DA1所成角的余弦值是( )A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)请你求出这种切割、焊接而成的长方体的最大容积V1;
(2)由于上述设计存在缺陷(材料有所浪费),请你重新设计切、焊方法,使材料浪费减少,而且所得长方体容器的容积V2>V1.

查看答案和解析>>
科目:高中数学 来源:2008-2009学年福建省泉州市惠安县惠南中学高二(上)期末数学试卷(选修2-1)(理科)(解析版) 题型:选择题
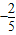


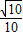
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com