
已知椭圆![]()
![]() 经过点
经过点![]() 其离心率为
其离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 相交于A、B两点,以线段
相交于A、B两点,以线段![]() 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆![]() 上,
上,![]() 为坐标原点.求
为坐标原点.求![]() 的取值范围.
的取值范围.
解:(Ⅰ)由已知可得![]() ,所以
,所以![]() ① ……………1分
① ……………1分
又点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ② ……………2分
② ……………2分
由①②解之,得![]() .
.
故椭圆![]() 的方程为
的方程为![]() . ……………5分
. ……………5分
(Ⅱ) 当![]() 时,
时,![]() 在椭圆
在椭圆![]() 上,解得
上,解得![]() ,所以
,所以![]()
![]() . ……6分
. ……6分
当![]() 时,则由
时,则由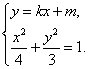
消![]() 化简整理得:
化简整理得:![]() ,
,
![]() ③ ……………8分
③ ……………8分
设![]() 点的坐标分别为
点的坐标分别为![]() ,则
,则
![]() . ……………9分
. ……………9分
由于点![]() 在椭圆
在椭圆![]() 上,所以
上,所以 ![]() . ……………1
. ……………1![]() 0分
0分
从而![]() ,化简得
,化简得![]() ,经检验满足③式.
,经检验满足③式.
………11分
又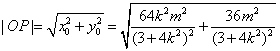

![]() ………………………12分
………………………12分
因为![]() ,得
,得![]() ,有
,有![]() ,
,
故![]() . ………………………13分
. ………………………13分
综上,所求![]() 的取值范围是
的取值范围是![]() . ………………………14分
. ………………………14分
(Ⅱ)另解:设![]() 点的坐标分别为
点的坐标分别为![]() ,
,
由![]() 在椭圆上,可得
在椭圆上,可得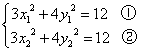 ………………………6分
………………………6分
①—②整理得![]() ………………………7分
………………………7分
由已知可得![]() ,所以
,所以 ……………………8分
……………………8分
由已知当![]() ,即
,即![]() ⑥ ………………………9分
⑥ ………………………9分
把④⑤⑥代入③整理得![]() ………………………10分
………………………10分
与![]() 联立消
联立消![]() 整理得
整理得![]() ……………………11分
……………………11分
由![]() 得
得![]() ,
,
所以![]() ……………………12分
……………………12分
因为![]() ,得
,得![]() ,有
,有![]() ,
,
故![]() . ………………………13分
. ………………………13分
所求![]() 的取值范围是
的取值范围是![]() . ………………………14分
. ………………………14分


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源:2012届云南省建水一中高三9月月考文科数学 题型:解答题
(本小题满分12分)
已知椭圆
 经过点
经过点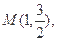 其离心率为
其离心率为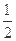
(1)求椭圆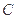 的方程
的方程
(2)设直线 与椭圆
与椭圆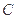 相交于A、B两点,以线段
相交于A、B两点,以线段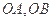 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆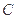 上,
上, 为坐标原点. 求
为坐标原点. 求 到直线
到直线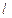 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省聊城市高三上学期1月份模块检测文科数学试卷(解析版) 题型:解答题
已知椭圆
 经过点
经过点 其离心率为
其离心率为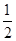 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设直线 与椭圆
与椭圆 相交于A、B两点,以线段
相交于A、B两点,以线段 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆 上,
上, 为坐标原点.求
为坐标原点.求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年云南省高三9月月考文科数学 题型:解答题
(本小题满分12分)
已知椭圆
 经过点
经过点 其离心率为
其离心率为
(1)求椭圆 的方程
的方程
(2)设直线 与椭圆
与椭圆 相交于A、B两点,以线段
相交于A、B两点,以线段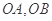 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆 上,
上, 为坐标原点. 求
为坐标原点. 求 到直线
到直线 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市海淀区高三下学期期中考试数学理卷 题型:解答题
(本小题共14分)
已知椭圆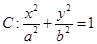
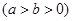 经过点
经过点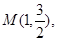 其离心率为
其离心率为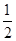 .
.
(Ⅰ)求椭圆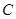 的方程;
的方程;
(Ⅱ)设直线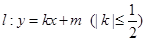 与椭圆
与椭圆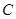 相交于A、B两点,以线段
相交于A、B两点,以线段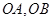 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆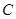 上,
上,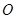 为坐标原点.求
为坐标原点.求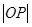 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com