
| A. | $\frac{7}{4}$ | B. | $\frac{7}{5}$ | C. | $\frac{15}{4}$ | D. | $\frac{5}{2}$ |
分析 根据向量数量积的公式和条件进行化简得到H是△ABC的垂心,结合三角形的边角关系进行求解即可.
解答 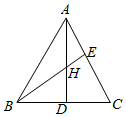 解:由题意知$\overrightarrow{PA}$•$\overrightarrow{PB}$+$\overrightarrow{PC}$•$\overrightarrow{PH}$=$\overrightarrow{PB}$•$\overrightarrow{PC}$+$\overrightarrow{PA}$•$\overrightarrow{PH}$,
解:由题意知$\overrightarrow{PA}$•$\overrightarrow{PB}$+$\overrightarrow{PC}$•$\overrightarrow{PH}$=$\overrightarrow{PB}$•$\overrightarrow{PC}$+$\overrightarrow{PA}$•$\overrightarrow{PH}$,
即$\overrightarrow{PB}$•($\overrightarrow{PA}$-$\overrightarrow{PC}$)+$\overrightarrow{PH}$•($\overrightarrow{PC}$-$\overrightarrow{PA}$)=0,即$\overrightarrow{CA}$•$\overrightarrow{HB}$=0.
同理得$\overrightarrow{AB}$•$\overrightarrow{HC}$=0,故H是△ABC的垂心,如图所示,
在Rt△CAD中,tan∠CAD=$\frac{3}{4}$,
∵∠CAD=∠CBE,
∴$\frac{DH}{3}$=$\frac{3}{4}$,即DH=$\frac{9}{4}$,
∴AH=4-$\frac{9}{4}$=$\frac{7}{4}$,
故选:A.
点评 本题主要考查向量数量积的应用,根据条件判断H是△ABC的垂心是解决本题的关键.综合性较强,考查学生的转化和运算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=|x| | B. | f(x)=-x3 | C. | f(x)=sinx-x | D. | f(x)=$\frac{1}{{x}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 38 | C. | 21 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
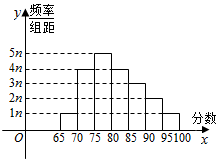 某班n名学生的综合素质测评成绩(百分制)频率分布直方图如图所示,已知70~80分数段的学生人数为27人,90~95分数段的学生中女生为2人.
某班n名学生的综合素质测评成绩(百分制)频率分布直方图如图所示,已知70~80分数段的学生人数为27人,90~95分数段的学生中女生为2人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 两个点 | B. | 一个椭圆 | C. | 一条线段 | D. | 两条直线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com