设a∈R,函数f(x)=3x3-4x+a+1.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若对于任意x∈[-2,0],不等式f(x)≤0恒成立,求a的最大值.
(Ⅰ)解:f(x)的导数f′(x)=9x
2-4.
令f′(x)>0,解得

,或
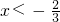
;
令f′(x)<0,解得

.
从而f(x)的单调递增区间为
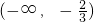
,

;
单调递减区间为(-

,

)
(Ⅱ)解:由f(x)≤0,得-a≥3x
3-4x+1
由(Ⅰ)得,函数y=3x
3-4x+1在(-2,

)内单调递增,
在(-

,0)内单调递减,
从而当x=-

时,函数y=3x
3-4x+1取得最大值

因为对于任意x∈[-2,0],不等式f(x)≤0恒成立,
故-a≥

,即a≤-

,
从而a的最大值是-

分析:(I)先求出函数f(x)的导函数fˊ(x),然后解不等式fˊ(x)>0和fˊ(x)<0,即可求出函数f(x)的单调区间;
(II)根据对于任意x∈[-2,0],不等式f(x)≤0恒成立,将a分离出来,然后研究另一侧函数的最值即可求出a的最值.
点评:本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减,以及函数恒成立问题,同时考查了转化与划归的数学思想,属于中档题.

 ,或
,或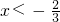 ;
; .
.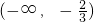 ,
, ;
; ,
, )
) )内单调递增,
)内单调递增, ,0)内单调递减,
,0)内单调递减, 时,函数y=3x3-4x+1取得最大值
时,函数y=3x3-4x+1取得最大值
 ,即a≤-
,即a≤- ,
,


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案