
抛掷一骰子,观察出现的点数,设事件A为“出现1点”,事件B为“出现2点”.已知P(A)=P(B)= ,则“出现1点或2点”的概率为( ).
,则“出现1点或2点”的概率为( ).
A. | B.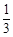 | C. | D. |
科目:高中数学 来源: 题型:单选题
两个实习生每人加工一个零件,加工为一等品的概率分别为 和
和 ,两个零件是否加工为一等品相互独立,则这两个零件中恰好有一个一等品的概率为( )
,两个零件是否加工为一等品相互独立,则这两个零件中恰好有一个一等品的概率为( )
A. | B. | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
从装有2个红球和2个白球的口袋里任取2个球,那么互斥而不对立的两个事件是
| A.至少1个白球,都是白球 |
| B.至少1个白球,至少1个红球 |
| C.至少1个白球,都是红球 |
| D.恰好1个白球,恰好2个白球 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
投掷一枚质地均匀的骰子两次,若第一次面向上的点数小于第二次面向上的点数我们称其为前效实验,若第二次面向上的点数小于第一次面向上的点数我们称其为后效实验,若两次面向上的点数相等我们称其为等效试验.那么一个人投掷该骰子两次后出现等效实验的概率是( )
A. | B.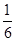 | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com