
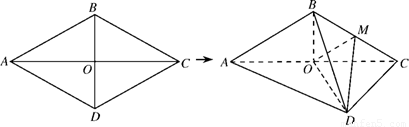
如图,菱形 的边长为4,
的边长为4,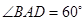 ,
, .将菱形
.将菱形 沿对角线
沿对角线 折起,得到三棱锥
折起,得到三棱锥 ,点
,点 是棱
是棱 的中点,
的中点,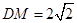 .
.

(1)求证: 平面
平面 ;
;
(2)求证:平面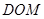
 平面
平面 ;
;
(3)求三棱锥 的体积.
的体积.
(1)详见解析;(2)详见解析;(3)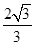 .
.
【解析】
试题分析:(1)利用三角形的中位线平行于相应的底边证明 ,然后结合直线与平面平行的判定定理即可证明
,然后结合直线与平面平行的判定定理即可证明 平面
平面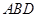 ;(2)先利用翻折时
;(2)先利用翻折时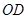 与
与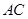 的相对位置不变证明
的相对位置不变证明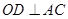 ,然后利用勾股定理证明
,然后利用勾股定理证明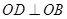 ,并结合直线与平面垂直的判定定理先证明
,并结合直线与平面垂直的判定定理先证明 平面
平面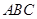 ,最终利用平面与平面垂直的判定定理证明平面
,最终利用平面与平面垂直的判定定理证明平面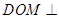 平面
平面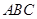 ;(3)利用(2)中的结论
;(3)利用(2)中的结论 平面
平面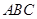 ,利用等体积法将三棱锥
,利用等体积法将三棱锥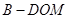 的体积转化为以点
的体积转化为以点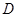 为顶点,
为顶点,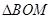 所在平面为底面的三棱锥
所在平面为底面的三棱锥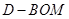 的体积来计算,则三棱锥的高为
的体积来计算,则三棱锥的高为 ,
,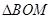 的面积为底面积,然后利用锥体的体积公式即可计算三棱锥
的面积为底面积,然后利用锥体的体积公式即可计算三棱锥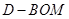 的体积,在计算
的体积,在计算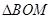 的面积时,首先应确定
的面积时,首先应确定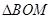 的形状,然后选择合适的公式计算计算
的形状,然后选择合适的公式计算计算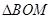 的面积.
的面积.
试题解析:(1)因为O为AC的中点,M为BC的中点,所以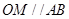 .
.
因为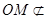 平面ABD,
平面ABD,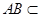 平面ABD,所以
平面ABD,所以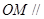 平面
平面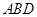 .
.
(2)因为在菱形ABCD中,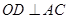 ,所以在三棱锥
,所以在三棱锥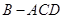 中,
中,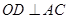 .
.
在菱形ABCD中,AB=AD=4,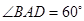 ,所以BD=4.因为O为BD的中点,
,所以BD=4.因为O为BD的中点,
所以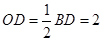 .因为O为AC的中点,M为BC的中点,所以
.因为O为AC的中点,M为BC的中点,所以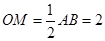 .
.
因为 ,所以
,所以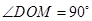 ,即
,即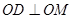 .
.
因为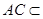 平面ABC,
平面ABC,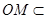 平面ABC,
平面ABC,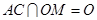 ,所以
,所以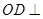 平面ABC.
平面ABC.
因为 平面DOM,所以平面
平面DOM,所以平面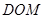
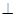 平面
平面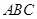 .
.
(3)由(2)得,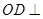 平面BOM,所以
平面BOM,所以 是三棱锥
是三棱锥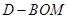 的高.
的高.
因为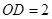 ,
, ,
,
所以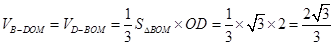 .
.
考点:直线与平面平行、平面与平面平行、等体积法


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
 如图,菱形ABCD的边长为4,∠BAD=60°,AC∪BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=2
如图,菱形ABCD的边长为4,∠BAD=60°,AC∪BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=2
如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
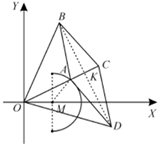 如图,在平面直角坐标系XOY中,菱形ABCD的边长为4,且|OB|=|OD|=6.
如图,在平面直角坐标系XOY中,菱形ABCD的边长为4,且|OB|=|OD|=6.查看答案和解析>>
科目:高中数学 来源:2014届广东省广州市越秀区高三上学期摸底考试理科数学试卷(解析版) 题型:解答题
如图,菱形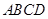 的边长为4,
的边长为4,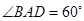 ,
,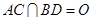 .将菱形
.将菱形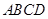 沿对角线
沿对角线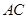 折起,得到三棱锥
折起,得到三棱锥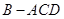 ,点
,点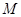 是棱
是棱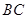 的中点,
的中点,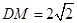 .
.
(1)求证: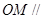 平面
平面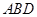 ;
;
(2)求证:平面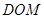
 平面
平面 ;
;
(3)求二面角 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com