
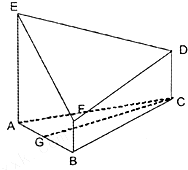
 已知△ABC是正三角形,GC是△ABC的中线,EA、FB、CD都垂直于平面ABC.EA=3a,AB=CD=2a,FB=a,设平面EDF与平面ABC的交线为l.
已知△ABC是正三角形,GC是△ABC的中线,EA、FB、CD都垂直于平面ABC.EA=3a,AB=CD=2a,FB=a,设平面EDF与平面ABC的交线为l. 证明:(1)取EF中点H,连DH,HG…1′
证明:(1)取EF中点H,连DH,HG…1′| |EA|+|BF| |
| 2 |
| 3a+a |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| (|MF|+|DN|) |
| 2 |
| 1 |
| 3 |
| (2a+a)2a |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
(本小题满分12分)
如图,在三棱锥D-ABC中,已知△BCD是正三角
形,AB⊥平面BCD,AB=BC=a,E为BC的中点,
F在棱AC上,且AF=3FC.
(1)求三棱锥D-ABC的表面积;
(2)求证AC⊥平面DEF;
(3)若M为BD的中点,问AC上是否存在一点N,
使MN∥平面DEF?若存在,说明点N的位置;若不
存在,试说明理由.

查看答案和解析>>
科目:高中数学 来源:正定中学2010高三下学期第一次考试(数学理) 题型:解答题
(本小题满分12分)
如图,在三棱锥D-ABC中,已知△BCD是正三角
形,AB⊥平面BCD,AB=BC=a,E为BC的中点,
F在棱AC上,且AF=3FC.
(1)求三棱锥D-ABC的表面积;
(2)求证AC⊥平面DEF;
(3)若M为BD的中点,问AC上是否存在一点N,
使MN∥平面DEF?若存在,说明点N的位置;若不
存在,试说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com