
分析 (1)假设a,b,c三数都小于2,则x+$\frac{1}{y}$+y+$\frac{1}{z}$+z+$\frac{1}{x}$<6,再结合基本不等式,引出矛盾,即可得出结论;
(2)运用分析法证明,运用不等式的性质和三角形的三边的关系,即可得证.
解答 证明:(1)假设a,b,c三数都小于2,则x+$\frac{1}{y}$+y+$\frac{1}{z}$+z+$\frac{1}{x}$<6.
∵x,y,z均大于0,
∴x+$\frac{1}{y}$+y+$\frac{1}{z}$+z+$\frac{1}{x}$=x+$\frac{1}{x}$+y+$\frac{1}{y}$+z+$\frac{1}{z}$≥2+2+2=6,矛盾.
∴a,b,c三数中至少有一个不小于2.
(2)要 证$\frac{a+b}{1+a+b}$>$\frac{c}{1+c}$成立,
只需证1-$\frac{1}{1+a+b}$>1-$\frac{1}{1+c}$
只需证-$\frac{1}{1+a+b}$>-$\frac{1}{1+c}$,
只需证-$\frac{1}{1+a+b}$<$\frac{1}{1+c}$只需证 1+c<1+a+b,只需证c<a+b
∵a,b,c是△ABC的三条边∴c<a+b成立,原不等式成立
点评 本题考查不等式的证明,考查分析法与反证法的运用,注意运用分析法证明,结合不等式的性质和三角形的三边关系,用反证法证明数学命题的方法和步骤,把要证的结论进行否定,得到要证的结论的反面,是解题的突破口,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{3}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{3\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,0) | C. | (0,∞) | D. | (0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| P(Χ2≥k) | 0.05 | 0.010 | 0.005 | 0.001 |
| K | 3.841 | 6.635 | 7.879 | 10.828 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年利润 | 1.2万元 | 1.0万元 | 0.9万元 |
| 频数 | 20 | 60 | 40 |
| 合格次数 | 2次 | 1次 | 0次 |
| 年利润 | 1.3万元 | 1.1万元 | 0.6万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
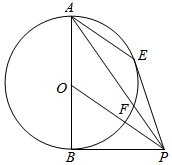 如图,AB是圆O的直径,PB是圆O的切线,过A点作AE∥OP交圆O于E点,PA交圆O于点F,连接PE.
如图,AB是圆O的直径,PB是圆O的切线,过A点作AE∥OP交圆O于E点,PA交圆O于点F,连接PE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com