
两种大小不同的钢板可按下表截成A,B,C三种规格成品:

某建筑工地需A,B,C三种规格的成品分别为15,18,27块,问怎样截这两种钢板,可
得所需三种规格成品,且所用钢板张数最小.
要截得所需三种规格的钢板,且使所截两种钢板的张数最少的方法有两种:
第一种截法是截第一种钢板3张,第二种钢板9张;
第二种截法是截第一种钢板4张,第二种钢板8张;
两种方法都最少要截两种钢板共12张.
设需要第一种钢板x张,第二种钢板y张,钢板总数为z张,z=x+y
约束条件为: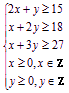
作出可行域如图所示:
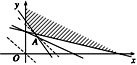
令z=0,作出基准直线l:y=-x,平行移动直线l发现在可行域内,经过直线x+3y=27和直线2x+y=15的交点A![]() 可使
可使
z取最小,由于![]() 都不是整数,而最优解(x,y)中,x,y必须都是整数,可行域内点A
都不是整数,而最优解(x,y)中,x,y必须都是整数,可行域内点A![]() 不是最优解;
不是最优解;
通过在可行域内画网格发现,经过可行域内的整点且与A![]() 点距离最近的直线是x+y=12,经过的整点是B(3,9)和
点距离最近的直线是x+y=12,经过的整点是B(3,9)和
C(4,8),它们都是最优解.
答 要截得所需三种规格的钢板,且使所截两种钢板的张数最少的方法有两种:
第一种截法是截第一种钢板3张,第二种钢板9张;
第二种截法是截第一种钢板4张,第二种钢板8张;
两种方法都最少要截两种钢板共12张.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板块数如下表:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 规格类型 钢板类型 |
A |
B |
C |
| 第一种钢板 | 2 | 1 | 1 |
| 第二种钢板 | 1 | 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
规格类型 钢板类型 |
A规格 | B规格 |
| 第一种钢板 | 2 | 1 |
| 第二种钢板 | 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
两种大小不同的钢板可按下表截成A,B,C三种规格成品:
|
| A规格 | B规格 | C规格 |
| 第一种钢板 | 2 | 1 | 1 |
| 第二种钢板 | 1 | 2 | 3 |
某建筑工地需A,B,C三种规格的成品分别为15,18,27块,问怎样截这两种钢板,可得所需三种规格成品,且所用钢板张数最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com