
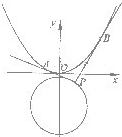
 如图,设点
如图,设点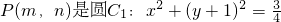 上的动点,过点P作抛物线
上的动点,过点P作抛物线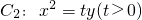 的两条切线,切点分别是A、B.已知圆C1的圆心M在抛物线C2的准线上.
的两条切线,切点分别是A、B.已知圆C1的圆心M在抛物线C2的准线上. 的最小值,以及取得最小值时点P的坐标.
的最小值,以及取得最小值时点P的坐标. ,
,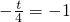 ,解得t=4.
,解得t=4.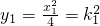 ;同理,x2=2k2,
;同理,x2=2k2,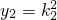 .
. =(x1-m)(x2-m)+(y1-n)(y2-n)
=(x1-m)(x2-m)+(y1-n)(y2-n)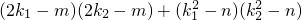
 -
-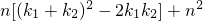
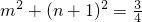 ,∴
,∴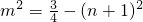 ,代入上式可得
,代入上式可得 =
=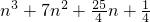 ,
,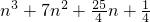
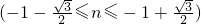 .
.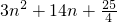 =
=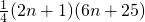 ,
,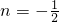 或
或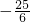 .
.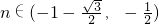 时,f′(n)<0,f(n)单调递减;
时,f′(n)<0,f(n)单调递减;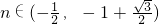 时,f′(n)>0,f(n)单调递增.
时,f′(n)>0,f(n)单调递增.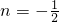 时,f(n)取得最小值
时,f(n)取得最小值 .
.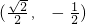 .
. ,再利用点P在圆上及函数的导数即可求出最小值.
,再利用点P在圆上及函数的导数即可求出最小值.

科目:高中数学 来源: 题型:
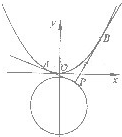 如图,设点P(m,n)是圆C1:x2+(y+1)2=
如图,设点P(m,n)是圆C1:x2+(y+1)2=| 3 |
| 4 |
| PA |
| PB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,F1、F2分别为椭圆C:
如图所示,F1、F2分别为椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且|MD|=
(2012•茂名一模)如图,设P是圆x2+y2=2上的动点,点D是P在x轴上的投影.M为线段PD上一点,且|MD|=
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省宁波市高三(上)期末数学试卷(理科)(解析版) 题型:解答题
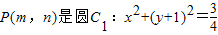 上的动点,过点P作抛物线
上的动点,过点P作抛物线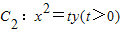 的两条切线,切点分别是A、B.已知圆C1的圆心M在抛物线C2的准线上.
的两条切线,切点分别是A、B.已知圆C1的圆心M在抛物线C2的准线上.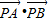 的最小值,以及取得最小值时点P的坐标.
的最小值,以及取得最小值时点P的坐标.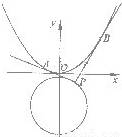
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com