解:(1)令x
1=x
2=0,得f(0)=f(x
0)+2f(0),∴f(x
0)=-f(0).①
令x
1=1,x
2=0,得f(x
0)=f(x
0)+f(1)+f(0),∴f(1)=-f(0).②
由①②得 f(x
0)=f(1).∴f(x)为单调函数,
∴x
0=1.
(2)由(1)得f(x
1+x
2)=f(x
1)+f(x
2)+f(1)=f(x
1)+f(x
2)+1.
∵f(n+1)=f(n)+f(1)+1=f(n)+2,f(1)=1,∴f(n)=2n-1.(n∈Z
*)
∴
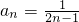
.
又∵
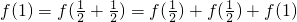
∴
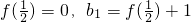
.
又
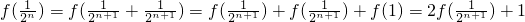
,
∴
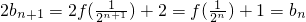
.
∴
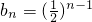
.
∴
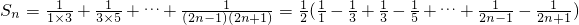
=
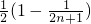
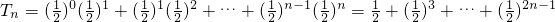
=
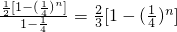
.
∴
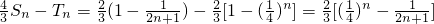
.
∵4
n=(3+1)
n=C
nn3
n+C
nn-13
n-1+…+C
n13+C
n0≥3n+1>2n+1,
∴
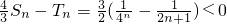
.
∴
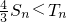
.
分析:(1)由题意对于任意实数x
1,x
2等式恒成立,故可采用赋值法求解;
(2)先证明{f(n)}是以1为首项,2为公差的等差数列,由此得
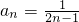
,从而可求S
n,再证{b
n}是等比数列从而可求T
n,代入
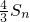
与T
n作差,利用二项式定理展开,进行放缩,即可求得结果.
点评:本题考查抽象函数的求值问题,一般采用赋值法解决,求数列的和,关键是求出其通项,再利用相应的求和公式,不等式中的恒成立问题,往往相应借助于函数的单调性解决.综合性较强,属难题.

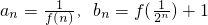 ,记Sn=a1a2+a2a3+…+anan+1,Tn=b1b2+b2b3+…+bnbn+1,比较
,记Sn=a1a2+a2a3+…+anan+1,Tn=b1b2+b2b3+…+bnbn+1,比较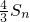 与Tn的大小关系,并给出证明.
与Tn的大小关系,并给出证明.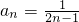 .
.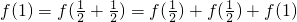
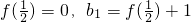 .
.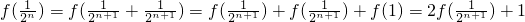 ,
,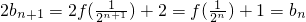 .
.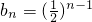 .
.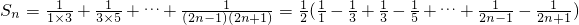
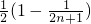
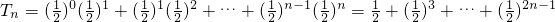
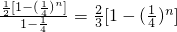 .
.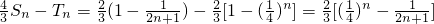 .
.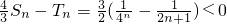 .
.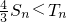 .
.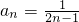 ,从而可求Sn,再证{bn}是等比数列从而可求Tn,代入
,从而可求Sn,再证{bn}是等比数列从而可求Tn,代入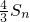 与Tn作差,利用二项式定理展开,进行放缩,即可求得结果.
与Tn作差,利用二项式定理展开,进行放缩,即可求得结果.
