
已知函数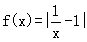
(Ⅰ)判断f(x)在 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(Ⅱ)若集合A={y | y=f(x), },B=[0,1], 试判断A与B的关系;
},B=[0,1], 试判断A与B的关系;
(Ⅲ)若存在实数a、b(a<b),使得集合{y | y=f(x),a≤x≤b}=[ma,mb],求非零实数m的取值范围.
(Ⅰ)f(x)在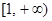 上为增函数.证明见解析(Ⅱ)A=B.(Ⅲ)
上为增函数.证明见解析(Ⅱ)A=B.(Ⅲ)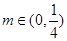
【解析】本题考查了函数单调性的定义,并结合着函数性质对区间进行分类讨论,并求解.分类讨论在高中范围内仍是很重要的一类思想,在高考中也是经常考查到的思想.
(1)由函数单调性的定义出发,给出证明.
(2)由x的范围算出f(x)的值域.再讲两个集合A和B进行比较.
(3)由前面单调性及函数特征的分析可知,0和1作为分类讨论的两个分界点分别讨论.
解:(1)f(x)在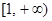 上为增函数.
上为增函数.
∵x≥1时,f(x)=1- 对任意的x1,x2,当1≤x1<x2时
对任意的x1,x2,当1≤x1<x2时
f(x1)- f(x2)=(1-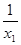 )-(1-
)-(1-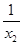 )=
)=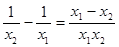
∵x1x2>0,x1-x2<0
∴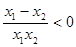 ∴f(x1)<
f(x2)
∴f(x1)<
f(x2)
∴f(x)在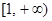 上为增函数.
上为增函数.
(2)证明f(x)在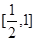 上单调递减,[1,2]上单调递增, 求出A=[0,1]说明A=B.
上单调递减,[1,2]上单调递增, 求出A=[0,1]说明A=B.
(3)∵a<b,ma<mb,∴m>0 ∵f(x)≥0, ∴ma≥0,又a≠0,∴a>0
1° 0<a<b≤1,由图象知,f(x)当x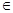 [a,b]递减,
[a,b]递减,
∴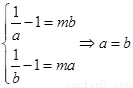 与a<b矛盾
与a<b矛盾
2° 0<a<1<b,这时f(1)=0,则ma=0,而ma>0 这亦与题设不符;
3°
1≤a<b,f(x)当x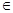 [a,b]递增
[a,b]递增
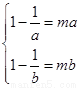 可知mx2-x+1=0在
可知mx2-x+1=0在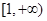 内有两不等实根
内有两不等实根
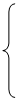 由
由 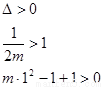 ,得
,得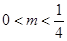
综上可知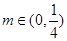


科目:高中数学 来源:2012-2013学年甘肃省高三上学期第二次月考数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知函数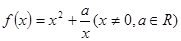
(1)判断函数 的奇偶性;
的奇偶性;
(2)若 在区间
在区间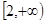 是增函数,求实数
是增函数,求实数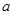 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三第二次月考文科数学 题型:选择题
已知函数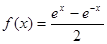 ,则下列判断中正确的是( )
,则下列判断中正确的是( )
A.奇函数,在R上为增函数 B.偶函数,在R上为增函数
C.奇函数,在R上为减函数 D.偶函数,在R上为减函数
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广西柳铁一中高三第三次月考文科数学试卷 题型:选择题
已知函数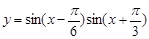 ,则下列判断正确的是( )
,则下列判断正确的是( )
A、其最小正周期为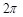 ,图象的一个对称中心是
,图象的一个对称中心是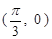
B、其最小正周期为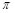 ,图象的一个对称中心是
,图象的一个对称中心是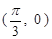
C、其最小正周期为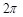 ,图象的一个对称中心是
,图象的一个对称中心是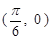
D、其最小正周期为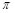 ,图象的一个对称中心是
,图象的一个对称中心是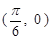
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com