
分析 (1)方程f(x)=-ax+m即为2lnx-x2+2ax-m=0,令g(x)=2lnx-x2+2ax-m,利用导数研究该函数在[,e]上的最小值,要使方程f(x)-ax+m=0在[$\frac{1}{e}$,e]上有两个不相等的实数根,得到关于m的不等式组,解之即可;
(2)将a用x1与x2表示,然后求出导函数f′(x),从而得到f′(px1+qx2),然后利用导数研究函数的单调性证明f′(px1+qx2)<0.
解答 解:(1)方程f(x)-ax+m=0即为2lnx-x2+m=0,
令g(x)=2lnx-x2+m,则g′(x)=$\frac{2}{x}$-2x=$\frac{-2(x+1)(x-1)}{x}$,
因为x∈[$\frac{1}{e}$,e],故g'(x)=0时,x=1.
当$\frac{1}{e}$<x<1时,g'(x)>0;当1<x<e时,g'(x)<0.
故函数g(x)在x=1处取得极大值g(1)=m-1,
又g($\frac{1}{e}$)=m-2-$\frac{1}{{e}^{2}}$,g(e)=m+2-e2,
g(e)-g($\frac{1}{e}$)=4-e2+$\frac{1}{{e}^{2}}$<0,则g(e)<g($\frac{1}{e}$),
故函数g(x)在[$\frac{1}{e}$,e]上的最小值是g(e).
方程f(x)-ax+m=0在[$\frac{1}{e}$,e]上有两个不相等的实数根,
则有 $\left\{\begin{array}{l}{g(1)=m-1>0}\\{g(\frac{1}{e})=m-2-\frac{1}{{e}^{2}}≤0}\end{array}\right.$,解得1<m≤2+$\frac{1}{{e}^{2}}$,
故实数m的取值范围是(1,2+$\frac{1}{{e}^{2}}$].
(2)∵函数f(x)的图象与x轴交于两个不同的点A(x1,0),B(x2,0),
2lnx-x2+ax=0的两个根为x1,x2,
则2lnx1-${{x}_{1}}^{2}$+ax1=0①,2lnx2-${{x}_{2}}^{2}$+ax2=0②,
两式相减得a=(x1+x2)-$\frac{2(l{nx}_{1}-l{nx}_{2})}{{{x}_{1}-x}_{2}}$,
f(x)=2lnx-x2+ax,f′(x)=$\frac{2}{x}$-2x+a,
则f′(px1+qx2)=$\frac{2}{{px}_{1}+{qx}_{2}}$-2(px1+qx2)+a=$\frac{2}{{px}_{1}+{qx}_{2}}$-$\frac{2(l{nx}_{1}-l{nx}_{2})}{{{x}_{1}-x}_{2}}$+(2p-1)(x2-x1).(*)
∵0<p≤q,p+q=1,则2p≤1,又0<x1<x2,∴(2p-1)(x2-x1)≤0,
下证 $\frac{2}{{px}_{1}+{qx}_{2}}$-$\frac{2(l{nx}_{1}-l{nx}_{2})}{{{x}_{1}-x}_{2}}$<0,
即证明 $\frac{{{x}_{2}-x}_{1}}{{px}_{1}+{qx}_{2}}$+ln$\frac{{x}_{1}}{{x}_{2}}$<0.
令t=$\frac{{x}_{1}}{{x}_{2}}$,∵0<x1<x2,∴0<t<1,
即证明u(t)=$\frac{1-t}{pt+q}$+lnt<0在0<t<1上恒成立,
∵u′(t)=$\frac{1}{t}$-$\frac{1}{{(pt+q)}^{2}}$=$\frac{{p}^{2}(t-1)(t-\frac{{q}^{2}}{{p}^{2}})}{{t(pt+q)}^{2}}$,
∵0<p≤q,∴$\frac{{q}^{2}}{{p}^{2}}$≥1,又0<t<1,∴u'(t)>0,
∴u(t)在(0,1)上是增函数,
则u(t)<u(1)=0,从而知 $\frac{{{x}_{2}-x}_{1}}{{px}_{1}+{qx}_{2}}$+ln$\frac{{x}_{1}}{{x}_{2}}$<0,
故(*)<0,即f'(px1+qx2)<0成立.
点评 本题主要考查了利用导数研究曲线上某点切线方程,以及利用导数研究函数的单调性,同时考查了转化的思想和计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
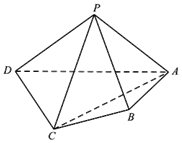 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=$\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
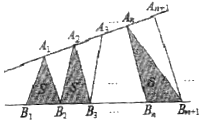 如图,点列{An},{Bn}分别在某个锐角的两边上,且|AnAn+1|=|An+1An+2|,An≠An+2,n∈N*,|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+2,n∈N*(P≠Q表示P与Q不重合).若dn=|AnBn|,Sn为△AnBnBn+1的面积,则( )
如图,点列{An},{Bn}分别在某个锐角的两边上,且|AnAn+1|=|An+1An+2|,An≠An+2,n∈N*,|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+2,n∈N*(P≠Q表示P与Q不重合).若dn=|AnBn|,Sn为△AnBnBn+1的面积,则( )| A. | {dn}是等差数列 | B. | {dn2}是等差数列 | C. | {Sn}是等差数列 | D. | {Sn2}是等差数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
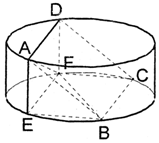 如图,圆柱的高为2,底面半径为3,AE,DF是圆柱的两条母线,B、C是下底面圆周上的两点,已知四边形ABCD是正方形.
如图,圆柱的高为2,底面半径为3,AE,DF是圆柱的两条母线,B、C是下底面圆周上的两点,已知四边形ABCD是正方形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com