练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如直线ax+by=R2与圆x2+y2=R2相交，则点（a，b）与此圆的位置关系是
    点在圆外
    点在圆外
    ．
    分析：根据直线与圆相交，得到圆心到直线的距离小于半径，利用点到直线的距离公式求出圆心到该直线的距离，得到关于a和b的关系式，再根据点与圆心的距离与半径比较即可得到点的位置．
    解答：解：由圆x2+y2=R2得到圆心坐标为（0，0），半径为R，
    ∵直线与圆相交，
    ∴圆心到直线的距离d=
    |-R2|
    		a2+b2
    ＜R，
    即a2+b2＞R2，即点到原点的距离大于半径，
    ∴点（a，b）在圆外部．
    故答案为：点在圆外
    点评：本题考查直线与圆的位置关系，点与圆的位置关系，本题解题的关键是运用点到直线的距离公式解决数学问题，本题的题设和结论交换位置以后可以得到另一个类似的题目．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2012•奉贤区一模）出租车几何学是由十九世纪的赫尔曼-闵可夫斯基所创立的．在出租车几何学中，点还是形如（x，y）的有序实数对，直线还是满足ax+by+c=0的所有（x，y）组成的图形，角度大小的定义也和原来一样．直角坐标系内任意两点A（x1，y1），B（x2，y2）定义它们之间的一种“距离”：|AB|=|x1-x2|+|y1-y2|，请解决以下问题：
    （1）求线段x+y=2（x≥0，y≥0）上一点M（x，y）的距离到原点O（0，0）的“距离”；
    （2）定义：“圆”是所有到定点“距离”为定值的点组成的图形，求“圆周”上的所有点到点Q（a，b）的“距离”均为 r的“圆”方程；
    （3）点A（1，3）、B（6，9），写出线段AB的垂直平分线的轨迹方程并画出大致图象．（说明所给图形小正方形的单位是1）

    查看答案和解析>>

    科目：高中数学 来源：上海市奉贤区2012届高三上学期期末调研测试数学文科试题 题型：044

    出租车几何学是由十九世纪的赫尔曼－闵可夫斯基所创立的．在出租车几何学中，点还是形如(x，y)的有序实数对，直线还是满足ax＋by＋c＝0的所有(x，y)组成的图形，角度大小的定义也和原来一样．直角坐标系内任意两点定义它们之间的一种“距离”：，请解决以下问题：

    1、(理)求线段上一点M(x，y)的距离到原点O(0，0)的“距离”；

    (文)求点A(1，3)、B(6，9)的“距离”；

    2、(理)定义：“圆”是所有到定点“距离”为定值的点组成的图形，求“圆周”上的所有点到点Q(a，b)的“距离”均为r的“圆”方程；

    (文)求线段上一点M(x，y)的距离到原点O(0，0)的“距离”；

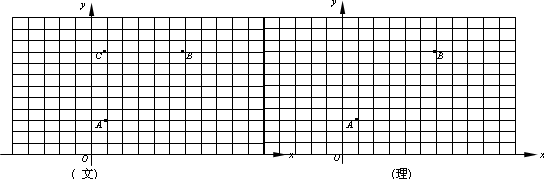
    3、(理)点A(1，3)、B(6，9)，写出线段AB的垂直平分线的轨迹方程并画出大致图像．

    (文)定义：“圆”是所有到定点“距离”为定值的点组成的图形，点A(1，3)、B(6，9)，C(1，9)，求经过这三个点确定的一个“圆”的方程，并画出大致图像；

    (说明所给图形小正方形的单位是1)

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    出租车几何学是由十九世纪的赫尔曼-闵可夫斯基所创立的．在出租车几何学中，点还是形如（x，y）的有序实数对，直线还是满足ax+by+c=0的所有（x，y）组成的图形，角度大小的定义也和原来一样．直角坐标系内任意两点A（x1，y1），B（x2，y2）定义它们之间的一种“距离”：|AB|=|x1-x2|+|y1-y2|，请解决以下问题：
    （1）求线段x+y=2（x≥0，y≥0）上一点M（x，y）的距离到原点O（0，0）的“距离”；
    （2）定义：“圆”是所有到定点“距离”为定值的点组成的图形，求“圆周”上的所有点到点Q（a，b）的“距离”均为 r的“圆”方程；
    （3）点A（1，3）、B（6，9），写出线段AB的垂直平分线的轨迹方程并画出大致图象．（说明所给图形小正方形的单位是1）

    查看答案和解析>>

    科目：高中数学 来源：2012年上海市奉贤区高考数学一模试卷（理科）（解析版） 题型：解答题

    出租车几何学是由十九世纪的赫尔曼-闵可夫斯基所创立的．在出租车几何学中，点还是形如（x，y）的有序实数对，直线还是满足ax+by+c=0的所有（x，y）组成的图形，角度大小的定义也和原来一样．直角坐标系内任意两点A（x1，y1），B（x2，y2）定义它们之间的一种“距离”：|AB|=|x1-x2|+|y1-y2|，请解决以下问题：
    （1）求线段x+y=2（x≥0，y≥0）上一点M（x，y）的距离到原点O（0，0）的“距离”；
    （2）定义：“圆”是所有到定点“距离”为定值的点组成的图形，求“圆周”上的所有点到点Q（a，b）的“距离”均为 r的“圆”方程；
    （3）点A（1，3）、B（6，9），写出线段AB的垂直平分线的轨迹方程并画出大致图象．（说明所给图形小正方形的单位是1）

    查看答案和解析>>

    同步练习册答案