
某专卖店销售一新款服装,日销售量(单位为件)f(n)与时间n(1≤n≤30、nÎ N*)的函数关系如下图所示,其中函数f(n)图象中的点位于斜率为5和-3的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.
(1)求f(n)的表达式,及前m天的销售总数;
(2)按以往经验,当该专卖店销售某款服装的总数超过 400件时,市面上会流行该款服装,而日销售量连续下降并低于30件时,该款服装将不再流行.试预测本款服装在市面上流行的天数是否会超过10天?请说明理由.

|
354件.10天. 1)根据题意,设 f (n) = (n Î N*), 而f(1)=2,∴5+a=2Þ a=-3. 又5m+a=-3m+b,∴b=8m+a=8m-3, ∴f(n)=nÎ N*). 由f(m)=57得m=12. ∴f(n)= ,(nÎ N*) 前12天的销售总量为5(1+2+3+…+12)-3×12=354件. (2)第13天的销售量为f(13)=-3×13+93=54件, 而354 +54>400件, ∴从第14天开始销售总量超过400件,即开始流行. 设第x天的日销售量开始低于30件(12<x≤30), 即f(x)=-3x+93<30, 解得x>21. ∴从第22天开始日销售量低于30件. ∵21-13=8, ∴该服装流行的时间不超过10天. |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
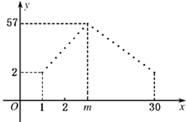 某专卖店销售一新款服装,日销售量(单位为件)f (n)与时间n(1≤n≤30、n∈N*)的函数关系如下图所示,其中函数f (n)图象中的点位于斜率为5和-3的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.
某专卖店销售一新款服装,日销售量(单位为件)f (n)与时间n(1≤n≤30、n∈N*)的函数关系如下图所示,其中函数f (n)图象中的点位于斜率为5和-3的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.查看答案和解析>>
科目:高中数学 来源:2010届广东华南师范大学附属中学高三模拟数学试题(三) 题型:解答题
(满分12分)某专卖店销售一新款服装,日销售量(单位为件)f (n) 与时间n(1≤n≤30、nÎ N*)的函数关系如下图所示,其中函数f (n) 图象中的点位于斜率为 5 和-3 的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.
(Ⅰ)求f (n) 的表达式,及前m天的销售总数;
(Ⅱ)按以往经验,当该专卖店销售某款服装的总数超过 400 件时,市面上会流行该款服装,而日销售量连续下降并低于 30 件时,该款服装将不再流行.试预测本款服装在市面上流行的天数是否会超过 10 天?请说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省白山市长白山一高高二(上)第二章综合检测数学试卷(解析版) 题型:解答题
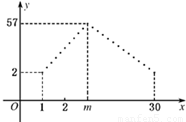 某专卖店销售一新款服装,日销售量(单位为件)f (n)与时间n(1≤n≤30、n∈N*)的函数关系如下图所示,其中函数f (n)图象中的点位于斜率为5和-3的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.
某专卖店销售一新款服装,日销售量(单位为件)f (n)与时间n(1≤n≤30、n∈N*)的函数关系如下图所示,其中函数f (n)图象中的点位于斜率为5和-3的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.查看答案和解析>>
科目:高中数学 来源:2010年广东省华南师大附中高考数学模拟试卷(三)(解析版) 题型:解答题
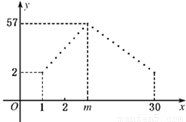 某专卖店销售一新款服装,日销售量(单位为件)f (n)与时间n(1≤n≤30、n∈N*)的函数关系如下图所示,其中函数f (n)图象中的点位于斜率为5和-3的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.
某专卖店销售一新款服装,日销售量(单位为件)f (n)与时间n(1≤n≤30、n∈N*)的函数关系如下图所示,其中函数f (n)图象中的点位于斜率为5和-3的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:2.12 函数的综合问题(解析版) 题型:解答题
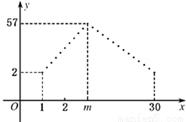 某专卖店销售一新款服装,日销售量(单位为件)f (n)与时间n(1≤n≤30、n∈N*)的函数关系如下图所示,其中函数f (n)图象中的点位于斜率为5和-3的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.
某专卖店销售一新款服装,日销售量(单位为件)f (n)与时间n(1≤n≤30、n∈N*)的函数关系如下图所示,其中函数f (n)图象中的点位于斜率为5和-3的两条直线上,两直线交点的横坐标为m,且第m天日销售量最大.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com