
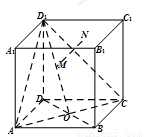
如图所示,正方体 的棱长为1,
的棱长为1,  分别是棱
分别是棱 ,
, 的中点,过直线
的中点,过直线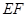 的平面分别与棱
的平面分别与棱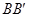 、
、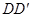 交于
交于 ,设
,设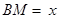 ,
, ,给出以下四个命题:
,给出以下四个命题:
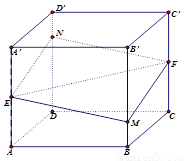
①平面
 平面
平面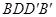 ;
;
②当且仅当 时,四边形
时,四边形 的面积最小;
的面积最小;
③四边形 周长
周长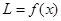 ,
, 是单调函数;
是单调函数;
④四棱锥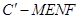 的体积
的体积 为常函数;
为常函数;
以上命题中真命题的序号为 。
①②④
【解析】
试题分析:①连结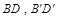 ,则由正方体的性质可知,
,则由正方体的性质可知,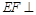 平面
平面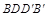 ,所以平面
,所以平面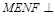 平面
平面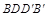 ,所以①正确;②连结
,所以①正确;②连结 ,因为
,因为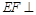 平面
平面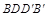 ,所以
,所以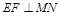 ,四边形
,四边形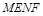 的对角线
的对角线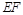 是固定的,所以要使面积最小,则只需
是固定的,所以要使面积最小,则只需 的长度最小即可,此时当
的长度最小即可,此时当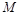 为棱的中点时,即
为棱的中点时,即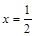 时,此时
时,此时 长度最小,对应四边形
长度最小,对应四边形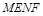 的面积最小.所以②正确;③因为
的面积最小.所以②正确;③因为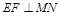 ,所以四边形
,所以四边形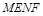 是菱形.当
是菱形.当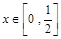 时,
时,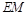 的长度由大变小.当
的长度由大变小.当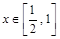 时,
时,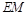 的长度由小变大.所以函数
的长度由小变大.所以函数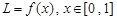 不单调.所以③错误;④连结
不单调.所以③错误;④连结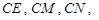 则四棱锥分割为两个小三棱锥,它们以
则四棱锥分割为两个小三棱锥,它们以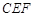 为底,以
为底,以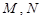 分别为顶点的两个小棱锥.因为
分别为顶点的两个小棱锥.因为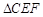 的面积是个常数,
的面积是个常数,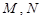 到平面
到平面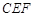 的距离是个常数,所以四棱锥
的距离是个常数,所以四棱锥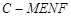 的体积
的体积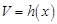 为常函数,所以④正确.所以选C.
为常函数,所以④正确.所以选C.
考点:1、空间点线面位置关系;2、空间几何体面积与体积的计算.


科目:高中数学 来源: 题型:
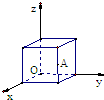 如图所示,正方体的棱长为1,点A是其一棱的中点,则点A在空间直角坐标系中的坐标是( )
如图所示,正方体的棱长为1,点A是其一棱的中点,则点A在空间直角坐标系中的坐标是( )A、(
| ||||
B、(1,1,
| ||||
C、(
| ||||
D、(1,
|
查看答案和解析>>
科目:高中数学 来源:2013-2014学年北京市海淀区高三上学期期末考试文科数学试卷(解析版) 题型:选择题
如图所示,正方体 的棱长为
的棱长为 ,
, ,
, 是线段
是线段 上的动点,过点
上的动点,过点 做平面
做平面 的垂线交平面
的垂线交平面 于点
于点 ,则点
,则点 到点
到点 距离的最小值为( )
距离的最小值为( )
A. B.
B.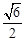 C.
C. D.
D.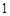
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省高三上学期期末考练习三理科数学试卷(解析版) 题型:填空题
如图所示,正方体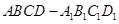 的棱长为1,
的棱长为1, 分别为线段
分别为线段 上的动点,则三棱锥
上的动点,则三棱锥 的体积为________.
的体积为________.
查看答案和解析>>
科目:高中数学 来源:2014届山东省济宁市高二上学期期末理科数学(解析版) 题型:选择题
如图所示,正方体 的棱长为1,O是平面
的棱长为1,O是平面 的中心,则O到平面
的中心,则O到平面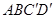 的距离是( )
的距离是( )
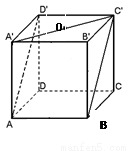
A. B.
B.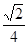 C.
C.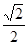 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014届广东省高一下期中理科数学试卷(解析版) 题型:选择题
如图所示,正方体的棱长为1,点A是其一棱的中点,则点A在空间直角坐标系中的坐标是( )
A. ( ,
, ,1) B. (1,1,
,1) B. (1,1, ) C. (
) C. ( ,1,
,1, ) D. (1,
) D. (1, ,1)
,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com