

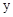 轴平行的线与函数图像只有一个交点,与
轴平行的线与函数图像只有一个交点,与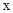 轴平行的线与函数有多个交点。所以根据函数定义,图A不是函数的图像,故选A
轴平行的线与函数有多个交点。所以根据函数定义,图A不是函数的图像,故选A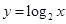 图像向上翻折得到
图像向上翻折得到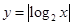 图像,B对;C选项可以是由
图像,B对;C选项可以是由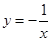 平移(向左)得到,故C正确;D选项函数解析式可知的是偶函数,并且定义域为
平移(向左)得到,故C正确;D选项函数解析式可知的是偶函数,并且定义域为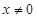 可以化为
可以化为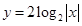 是
是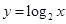 图像关于
图像关于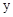 轴先对称后伸缩得到,所以D正确。答案选择A
轴先对称后伸缩得到,所以D正确。答案选择A

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com