
已知函数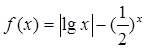 有两个零点
有两个零点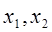 ,则有( )
,则有( )
A.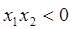 | B.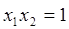 | C.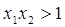 | D.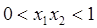 |
D
解析分析:先将f(x)=|lgx|-( )x有两个零点转化为y=|lgx|与y=2-x有两个交点,然后在同一坐标系中画出两函数的图象得到零点在(0,1)和(1,+∞)内,即可得到-2-x1=lgx1和2-x2="lg" x2,然后两式相加即可求得x1x2的范围.
)x有两个零点转化为y=|lgx|与y=2-x有两个交点,然后在同一坐标系中画出两函数的图象得到零点在(0,1)和(1,+∞)内,即可得到-2-x1=lgx1和2-x2="lg" x2,然后两式相加即可求得x1x2的范围.
解:f(x)=|lgx|-( )x有两个零点x1,x2
)x有两个零点x1,x2
即y=|lgx|与y=2-x有两个交点
由题意x>0,分别画y=2-x和y=|lgx|的图象
发现在(0,1)和(1,+∞)有两个交点
不妨设 x1在(0,1)里 x2在(1,+∞)里
那么 在(0,1)上有 2-x1=-lgx1,即-2-x1=lgx1…①
在(1,+∞)有2-x2="lg" x2…②
①②相加有2-x2-2-x1=lgx1x2
∵x2>x1,∴2-x2<2-x1即2-x2-2-x1<0
∴lgx1x2<0
∴0<x1x2<1
故选D.


科目:高中数学 来源: 题型:单选题
设g(x)是函数f(x)=ln(x+1)+2x的导函数,若函数g(x)按向量a平移后得到函数y=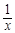 ,则向量a等于
,则向量a等于
| A.(1,2) | B.(-1,-2) | C.(-2,-1) | D.(2,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com