
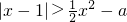 仅有负数解,则实数a的取值范围是________.
仅有负数解,则实数a的取值范围是________. ,-1]
,-1]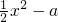 的图象,当y=|x-1|过点(0,-a)时,求出a的值;当y=
的图象,当y=|x-1|过点(0,-a)时,求出a的值;当y=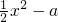 和直线y=-x+1相切时,求出a的值,数形结合可得实数a的取值范围.
和直线y=-x+1相切时,求出a的值,数形结合可得实数a的取值范围.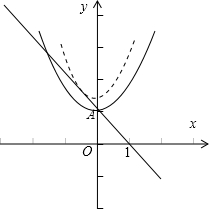 解:在同一坐标系画出函数y=|x-1|和 y=
解:在同一坐标系画出函数y=|x-1|和 y=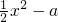 的图象,
的图象,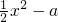 和直线y=-x+1相切时,-x+1=
和直线y=-x+1相切时,-x+1=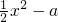 ,即x2+2x-2a-2=0,
,即x2+2x-2a-2=0, .
. ,-1],
,-1], ,-1].
,-1].

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com