练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知椭圆C：(a＞b＞0)经过点P(1，)，且两焦点与短轴的一个端点构成等腰直角三角形．

    (1)求椭圆的方程；

    (2)动直线l：mx＋ny＋n＝0(m，n∈R)．交椭圆C于A、B两点，求证：以AB为直径的动圆恒经过定点(0，1)．

    答案：
    解析：

    　　解：(1)∵椭圆的两焦点与短轴的一个端点的连线构成等腰直角三角形，

    　　∴∴

    　　又∵椭圆经过点，代入可得，∴

    　　故所求椭圆方程为　3分

    　　(2)首先求出动直线过(0，)点．5分

    　　当L与x轴平行时，以AB为直径的圆的方程：

    　　，此圆过点T(0，1)

    　　当L与x轴垂直时，以AB为直径的圆的方程：，

    　　此圆过点T(0，1)　7分

    　　由

    　　设点、　10分

    　　

    　　

    　　

    　　

    　　所以TA⊥TB，即以AB为直径的圆恒过点T(0，1)

    　　所以在坐标平面上存在一个定点T(0，1)满足条件．12分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知椭圆C:=1(a＞b＞0),直线l1:=1被椭圆C截得的弦长为2，过椭圆C的右焦点且斜率为3的直线l2被椭圆C截得的弦长是椭圆长轴长的，求椭圆C的方程.

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷（解析版） 题型：解答题

    已知椭圆C: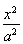+=1(a>b>0)的一个顶点为A(2,0),离心率为.直线y=k(x-1)与椭圆C交于不同的两点M,N.

    (1)求椭圆C的方程;

    (2)当△AMN的面积为时,求k的值.

     

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年人教版高考数学文科二轮专题复习提分训练22练习卷（解析版） 题型：选择题

    已知椭圆C:+=1(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若|AB|=10,|BF|=8,cos∠ABF=,则C的离心率为(　　)

    (A) (B) (C) (D)

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年广东省高三8月第一次月考文科数学试卷（解析版） 题型：解答题

    （本题满分14分）

    已知椭圆C：(a＞b＞0)的离心率为,短轴一个端点到右焦点的距离为3.

    (1)求椭圆C的方程;

    (2)过椭圆C上的动点P引圆O：x2+y2=b2的两条切线PA、PB，A、B分别为切点，试探究椭圆C上是否存在点P，由点P向圆O所引的两条切线互相垂直？若存在，请求出点P的坐标；若不存在，请说明理由.

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011年辽宁省高二上学期期末考试数学文卷 题型：解答题

    (本小题满分12分)

    已知椭圆C:（a＞b＞0）的离心率为短轴一个端点到右焦点的

    距离为.

    (Ⅰ)求椭圆C的方程;    

    (Ⅱ)设直线l与椭圆C交于A、B两点，坐标原点O到直线l的距离为，求△AOB面积的

    最大值.

     

    查看答案和解析>>

    同步练习册答案