
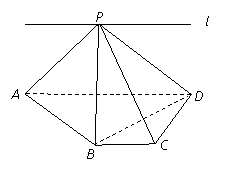
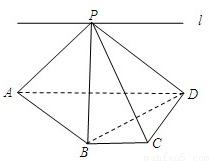
(14分)如图,ABCD为直角梯形,∠C=∠CDA=![]() ,AD=2BC=2CD,P为平面ABCD外一点,且PB⊥BD.
,AD=2BC=2CD,P为平面ABCD外一点,且PB⊥BD.
⑴ 求证:PA⊥BD;
(2) 若![]() 与CD不垂直,求证:
与CD不垂直,求证:![]() ;
;
⑶ 若直线l过点P,且直线l∥直线BC,试在直线l上找一点E,
使得直线PC∥平面EBD.
解析:(1)![]() ABCD为直角梯形,AD =
ABCD为直角梯形,AD =![]() ,
,![]() AB⊥BD,(1分)
AB⊥BD,(1分)
PB⊥BD ,AB![]() PB =B,AB,PB
PB =B,AB,PB![]() 平面PAB,BD⊥平面PAB,( 4分)
平面PAB,BD⊥平面PAB,( 4分)
PA![]() 面PAB,
面PAB,![]() PA ⊥BD.(5分)
PA ⊥BD.(5分)
(2)假设PA=PD,取AD 中点N,连PN,BN,则PN⊥AD,BN⊥AD, (7分)
AD⊥平面PNB,得 PB⊥AD,(8分)
又PB⊥BD ,得PB⊥平面ABCD,
∴![]() (9分)
(9分)
又∵![]() ,∴CD⊥平面PBC,
,∴CD⊥平面PBC,
∴CD⊥PC, 与已知条件![]() 与
与![]()
不垂直矛盾
∴![]() (10分)
(10分)
(3)在上l取一点E,使PE=BC,(11分)
![]() PE∥BC,
PE∥BC,![]() 四边形BCPE是平行四边形,(12分)
四边形BCPE是平行四边形,(12分)
![]() PC∥BE,PC
PC∥BE,PC![]() 平面EBD, BE
平面EBD, BE![]() 平面EBD
平面EBD


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
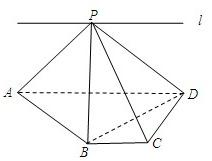 如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD,P为平面ABCD外一点,且PB⊥BD.
如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD,P为平面ABCD外一点,且PB⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:
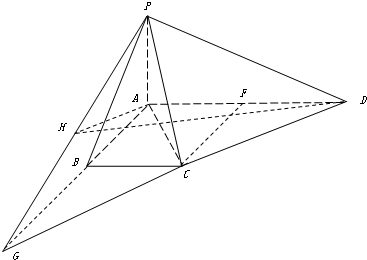 如图,ABCD为直角梯形,∠DAB=∠ABC=90°,AB=BC=1,AD=2,PA⊥平面ABCD,PA=1.
如图,ABCD为直角梯形,∠DAB=∠ABC=90°,AB=BC=1,AD=2,PA⊥平面ABCD,PA=1.查看答案和解析>>
科目:高中数学 来源:2010年江苏省高三数学中等生强化练习(7)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010年高考数学小题限时训练试卷(12)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com