分析:(1)先根据题意结合题中条件找出已知直线的中位线即证明线线平行,再说明其中一条直线在平面内,则可证明线面平行.
(2)由其中一个平面内一点作另一个平面的垂线,再由垂足向交线作垂线,进而连线得到二面角的平面角,然后证明这个角就是二面角的平面角,最后利用解三角形的知识求出二面角即可.
解答: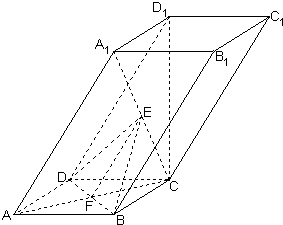
解:(1)连接AC,与BD交于点F,连接EF,
在矩形ABCD中,F为AC的中点,又E为A
1C的中点,
∴A
1A∥EF,
又在平行六面体ABCD-A
1B
1C
1D
1中,C
1C∥A
1A,
∴C
1C∥EF,又EF?平面BDE,C
1C?平面BDE,
∴直线C
1C∥平面BDE.
(2)连接A
1B,BD
1,∵在平行六面体ABCD-A
1B
1C
1D
1中,A
1D
1与BC平行且相等,
∴四边形A
1BCD
1是平行四边形,则A
1C与BD
1互相平分,
∴A
1C的中点E也是BD
1的中点.取BC的中点F,连接EF,则EF∥D
1C,且
EF=D1C=1,
又D
1C⊥平面ABCD,
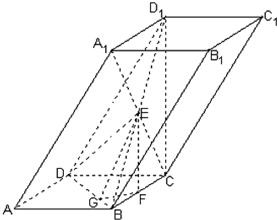
∴EF⊥平面ABCD,过点F作FG垂直BD于点G,连接EG.
根据三垂线定理有EG⊥BD,故∠EGF是二面角E-BD-C的平面角
在Rt△BCD中,
sin∠DBC===,
∴在Rt△FGB中,
FG=FB•sin∠DBC=,
∴在Rt△EFG中,
tan∠EGF===.
点评:解决此类问题的关键是熟悉几何体的结构特征,正确确定几何体中线面垂直关系与线面平行关系,进而解决问题.

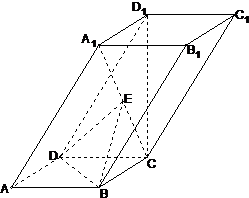 如图,四棱柱ABCD-A1B1C1D1的底面是矩形,D1C⊥平面ABCD,AB=1,BC=D1C=2,E为A1C的中点.
如图,四棱柱ABCD-A1B1C1D1的底面是矩形,D1C⊥平面ABCD,AB=1,BC=D1C=2,E为A1C的中点. 解:(1)连接AC,与BD交于点F,连接EF,
解:(1)连接AC,与BD交于点F,连接EF,


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案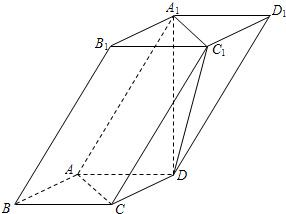 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱AA1=2.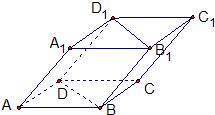 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且∠A1AD=∠A1AB=60°,则侧棱AA1和截面B1D1DB的距离是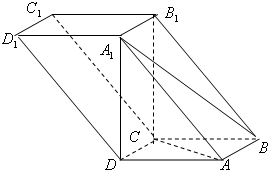 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2,
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为1的正方形,侧棱A1A=2, (2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.
(2013•泉州模拟)如图,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD. (2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,
(2013•天津)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,