
设f(x)=ln(x2+1),g(x)=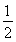 x2-
x2- .
.
(1)求F(x)=f(x)-g(x)的单调区间,并证明对[-1,1]上的任意x1,x2,x3,都有F(x1)+F(x2)>F(x3);
(2)将y=f(x)的图像向下平移a(a>0)个单位,同时将y=g(x)的图像向上平移b(b>0)个单位,使它们恰有四个交点,求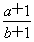 的取值范围.
的取值范围.
(1)在(-∞,-1)和(0,1)上单调递增,在(-1,0)和(1,+∞)上单调递减,证明见解析(2)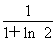 <
<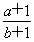 <1+ln 2
<1+ln 2
【解析】(1)F(x)=ln(x2+1)- x2-
x2- ,
,
F′(x)=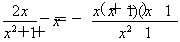 .
.
F′(x),F(x)的值随x值的变化如下表:
x | (-∞,-1) | (-1,0) | (0,1) | (1,+∞) |
F′(x) | + | - | + | - |
F(x) | ↗ | ↘ | ↗ | ↘ |
故F(x)在(-∞,-1)和(0,1)上单调递增,在(-1,0)和(1,+∞)上单调递减,在[-1,1]上F(x)的最小值F(x)min=F(0)= .
.
F(x)的最大值F(x)max=F(1)=F(-1)=ln 2.
因此F(x1)+F(x2)≥2F(x)min=1,
而F(x3)≤F(x)max=ln 2,
故F(x1)+F(x2)>F(x3).
(2)由题意可知y=ln(x2+1)-a与y= x2-
x2- +b的图像恰有四个交点.
+b的图像恰有四个交点.
由ln(x2+1)-a= x2-
x2- +b,
+b,
则a+b=ln(x2+1)- x2+
x2+ .
.
令F(x)=ln(x2+1)- x2+
x2+ ,
,
由(1)可知F(x)极小值=F(0)= ,F(x)极大值=F(1)=ln 2.又F(4)=F(-4)<0<F(0),所以F(x)的大致图像如图所示,
,F(x)极大值=F(1)=ln 2.又F(4)=F(-4)<0<F(0),所以F(x)的大致图像如图所示,

图(1)
要使y=a+b与y=F(x)恰有四个交点,则 <a+b<ln 2.
<a+b<ln 2.
由
得到(b,a)的可行域为如图(2)所示的阴影部分.

图(2)
又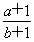 可视为点P(-1,-1)与可行域内的点连线的斜率,
可视为点P(-1,-1)与可行域内的点连线的斜率,
故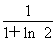 <
<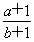 <1+ln 2.
<1+ln 2.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集3A讲练习卷(解析版) 题型:选择题
已知点P(x,y)满足 则点Q(x+y,y)构成的图形的面积为( )
则点Q(x+y,y)构成的图形的面积为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集1B讲练习卷(解析版) 题型:选择题
若集合A={0,1},B={-1,a2},则“a=1”是“A∩B={1}”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集19讲练习卷(解析版) 题型:填空题
设f(x)是定义在R上的偶函数,且当x≥0时,f(x)=2x.若对任意的x∈[a,a+2],不等式f(x+a)≥f2(x)恒成立,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集19讲练习卷(解析版) 题型:选择题
“a≤0”是“函数f(x)=|(ax-1)x|在区间(0,+∞)内单调递增”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集18讲练习卷(解析版) 题型:填空题
若曲线y=x-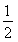 在点(m,m-
在点(m,m-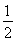 )处的切线与两坐标轴围成三角形的面积为18,则m=________.
)处的切线与两坐标轴围成三角形的面积为18,则m=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集18讲练习卷(解析版) 题型:选择题
F1,F2是双曲线C: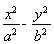 =1(a>0,b>0)的两个焦点,过左焦点F1的直线l与双曲线C的左、右两支分别交于A,B两点.若|AB|∶|BF2|∶|AF2|=3∶4∶5,则双曲线的离心率是( )
=1(a>0,b>0)的两个焦点,过左焦点F1的直线l与双曲线C的左、右两支分别交于A,B两点.若|AB|∶|BF2|∶|AF2|=3∶4∶5,则双曲线的离心率是( )
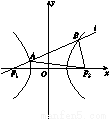
A.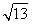 B.
B.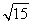 C.2 D.
C.2 D.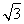
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集17讲练习卷(解析版) 题型:选择题
已知回归直线斜率的估计值为1.23,样本点的中心为点(4,5),则回归直线的方程为( )
A.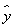 =1.23x+4 B.
=1.23x+4 B.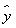 =1.23x+5
=1.23x+5
C. =1.23x+0.08 D.
=1.23x+0.08 D.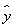 =0.08x+1.23
=0.08x+1.23
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集14讲练习卷(解析版) 题型:选择题
抛物线y2=8x的准线与双曲线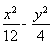 =1的两条渐近线围成的三角形的面积为( )
=1的两条渐近线围成的三角形的面积为( )
A.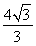 B.
B.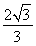 C.
C. 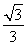 D.2
D.2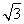
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com